COME RISOLVERE LE DISEQUAZIONI IRRAZIONALI: CASI PARTICOLARI
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- Disequazioni irrazionali
- Disequazioni irrazionali con lo zero a secondo membro
- Disequazioni irrazionali con una costante a secondo membro e segno di minore
- Disequazioni irrazionali con una costante a secondo membro e segno di maggiore
- Disequazioni irrazionali con un polinomio a secondo membro e segno di minore
- Disequazioni irrazionali con un polinomio a secondo membro e segno di maggiore
Nelle lezioni precedenti abbiamo visto come si risolvono le DISEQUAZIONI IRRAZIONALI.
I casi da noi esaminati riguardano:
- disequazioni nelle quali troviamo un
radicale al primo membro e lo zero a secondo membro
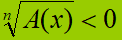
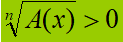
- disequazioni
nelle quali troviamo un radicale a primo membro ed una costante
all'altro membro
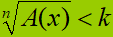
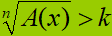
- disequazioni nelle quali troviamo un radicale a primo membro ed un polinomio all'altro membro
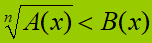
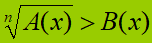
Ora chiediamoci: "Se ci troviamo di fronte ad una disequazione irrazionale che si presenta in una forma diversa rispetto a quelle viste, come la risolviamo?"
Nella maggior parte dei casi, per poterle risolvere, esse si devono RICONDURRE ad UNA DELLE FORME VISTE in precedenza con degli opportuni accorgimenti.
Nelle prossime lezioni vedremo come si possono risolvere disequazioni che si presentano con le seguenti forme:
- con un radicale ed un polinomio nello stesso membro;
- con due o più radicali;
- con due o più radicali con indici diversi;
- con una frazione che contiene a numeratore o a denominatore un radicale (ma anche sia a numeratore che a denominatore) e con l'incognita a denominatore;
- con una radice di radice.






