DISEQUAZIONI CON RADICE DI RADICE
Concludiamo le lezioni dedicate alle DISEQUAZIONI IRRAZIONALI andando a vedere come si risolvono le DISEQUAZIONI nelle quali compaiono delle RADICI di RADICI.
Il modo di procedere dipende da come si presenta la disequazione. In ogni caso occorre cercare di trasformare la disequazione in uno dei tipi consueti che abbiamo già esaminato.
In genere si procede con un ELEVAMENTO A POTENZA in modo da eliminare la radice più esterna.
Inoltre bisogna sempre ricordare che, in presenza di RADICALI DI INDICE PARI è necessario porre la condizione che il relativo radicando sia MAGGIORE o UGUALE a ZERO.
Vediamo due esempi per capire meglio il concetto.
Esempio 1:
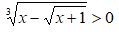
La radice più esterna è di indice dispari (n = 3) quindi il relativo radicando potrà essere sia positivo che negativo, ma anche pari a zero.
Non avendo particolari condizioni da porre eleviamo primo e secondo membro al cubo in modo da eliminare la radice più estera:
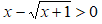
Isoliamo la radice a primo membro portando tutto il resto a secondo membro, ricordandoci di cambiare il segno:
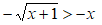
Cambiamo il segno di entrambi i membri e il verso della disequazione:
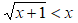
Abbiamo ricondotto la nostra disequazione alla forma
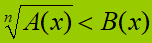
dove n, nel nostro caso, è PARI.
Sappiamo che, per risolvere questo tipo di disequazione dobbiamo impostare il sistema:
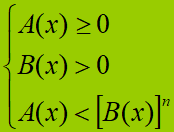
Nel nostro esempio dovremo impostare il seguente sistema:
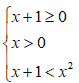
Lasciamo a voi eseguire i calcoli.
Esempio 2:
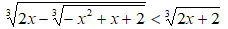
Qui abbiamo tutte radici di indice dispari (n = 3) quindi non dobbiamo porre particolari condizioni per elevare primo e secondo membro al cubo in modo da eliminare la radice più estera:
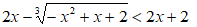
Isoliamo la radice a primo membro:
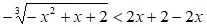
Eseguiamo un po' di calcoli e cambiamo di segno:
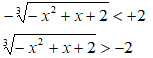
Abbiamo ricondotto la nostra disequazione al tipo
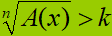
con n DISPARI.
Questo tipo di disequazioni si risolvono elevando primo e secondo membro alla ennesima potenza. Ovvero:
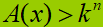
Nel nostro caso, quindi, dovremo risolvere la seguente disequazione:
- x2 + x + 2 > -8.
Anche questa volta lasciamo a voi risolvere la disequazione.






