DISEQUAZIONI IRRAZIONALI CON UN RADICALE ED UN POLINOMIO NELLO STESSO MEMBRO
- Disequazioni irrazionali
- Disequazioni irrazionali con un polinomio a secondo membro e segno di maggiore
- Come si risolvono le disequazioni irrazionali
- Come risolvere le disequazioni irrazionali: casi particolari
Continuiamo a vedere come possiamo risolvere le DISEQUAZIONI IRRAZIONALI esaminando i casi nei quali esse non si presentano in una delle forme classiche viste nelle lezioni precedente.
In questa lezione ci soffermiamo sul caso in cui la disequazione si presenta con un RADICALE ed un POLINOMIO nello stesso membro.
Primo caso. La disequazione si presenta nel modo seguente:
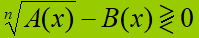
Nel nostro esempio abbiamo supposto di avere
- B(x)
ma quanto diremo in tutta la lezione vale sia nel caso in cui troviamo -B(x) che nel caso in cui troviamo +B(x).
Se portiamo B(x) a SECONDO MEMBRO, cambiandogli di segno, riconduciamo la nostra disequazione ad una delle forme già viste nelle precedenti lezioni:

Esempio:
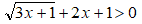
Isoliamo il radicale a primo membro, portando 2x + 1 a secondo membro e ricordandoci di cambiargli di segno.
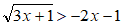
In questo modo abbiamo trasformato la nostra disequazione in una disequazione irrazionale con un polinomio a secondo membro e segno di maggiore. Quindi si tratterà di risolvere l'unione dei due sistemi:
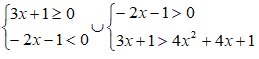
Lasciamo a voi i calcoli. Vi diciamo solamente che il risultato della nostra disquazione è
x ≥ 1/3.
Secondo caso. La disequazione si presenta nel modo seguente:
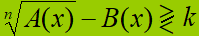
Anche in questo caso portiamo B(x) a SECONDO MEMBRO, cambiandogli di segno e riconduciamo la nostra disequazione ad una delle forme già viste nelle precedenti lezioni:
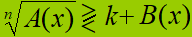
Esempio:
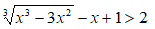
Isoliamo il radicale a primo membro, portando -x + 1 a secondo membro e ricordandoci di cambiargli di segno.
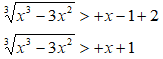
In questo modo abbiamo trasformato la nostra disequazione in una disequazione irrazionale con un polinomio a secondo membro e segno di maggiore. Ora basterà elevare entrambi i membri della disequazione alla terza:
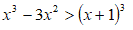
Lasciamo a voi i calcoli. Il risultato della nostra disquazione è
x < 1/3.
Terzo caso. La disequazione si presenta nel modo seguente:
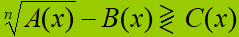
Anche in questo caso portiamo B(x) a SECONDO MEMBRO, cambiandogli di segno, quindi andiamo a SOMMARE i TERMINI SIMILI e avremo ricondotto la nostra disequazione ad una delle forme già viste nelle precedenti lezioni:
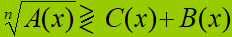
Esempio:
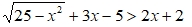
Isoliamo il radicale a primo membro, portando 3x - 5 a secondo membro e ricordandoci di cambiargli di segno.
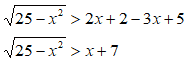
In questo modo abbiamo trasformato la nostra disequazione in una disequazione irrazionale con un polinomio a secondo membro e segno di maggiore. Quindi si tratterà di risolvere l'unione dei due sistemi:
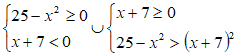
Il risultato è
3< x < 4.






