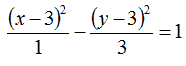EQUAZIONE DELL'IPERBOLE TRASLATA DATO IL CENTRO ED UN PUNTO
- L'iperbole
- Equazione dell'iperbole
- Elementi dell'iperbole
- Iperbole traslata
- Fuochi, vertici e asintoti dell'iperbole traslata
Continuiamo a parlare dell'IPERBOLE TRASLATA: in questa lezione vedremo come trovare la sua equazione quando conosciamo le coordinate del centro.
Esempio:
scrivere l'equazione dell'iperbole traslata con centro nel punto P0 di coordinate (3; 3), passante per il punto P di coordinate (1; 6) e il cui asse traverso è parallelo all'asse delle x ed è pari a 2. Quindi trovare i fuochi e i vertici dell'iperbole.
Iniziamo col dire che sappiamo che l'asse traverso dell'iperbole è parallelo all'asse delle x: questo significa che i fuochi si trovano su una retta parallela all'asse delle x.
Di conseguenza, la formula da applicare per trovare l'EQUAZIONE DELL'IPERBOLE TRASLATA è la seguente:
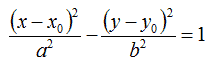
In questa equazione x0 e y0 rappresentano le coordinate del centro. Quindi, nel nostro caso abbiamo:
x0 = 3
y0 = 3.
Sostituendo nella formula precedente abbiamo:
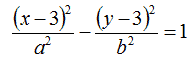
Ora dobbiamo trovare i valori di a2 e b2. Ma noi sappiamo che l'asse traverso è 2 e, come è noto l'asse traverso è pari a 2a, quindi
a = 1
e, di conseguenza:
a2 = 1.
Quindi possiamo scrivere:
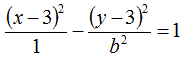
Sappiamo anche che la nostra iperbole passa per il punto P(1; 6). Di conseguenza, l'iperbole, quando passa per tale punto diventa:
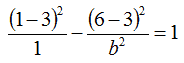
Eseguendo i calcoli troviamo il valore di b2:
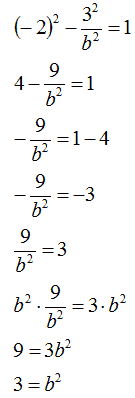
Quindi, l'equazione della nostra iperbole è: