EQUAZIONE DELL'IPERBOLE DATI IL FUOCO E UN PUNTO
- L'iperbole
- Equazione dell'iperbole
- Elementi dell'iperbole
- Asintoti dell'iperbole
- Proprietà dell'iperbole
- Come disegnare un'iperbole
- Eccentricità dell'iperbole
- Iperbole con fuochi sull'asse delle y
- Elementi dell'iperbole con fuochi sull'asse delle y
- Sistemi di equazioni di secondo grado
- Risoluzione delle equazioni di secondo grado complete
Vediamo ora come risolvere quei problemi nei quali ci viene chiesto di scrivere l'EQUAZIONE DELL'IPERBOLE conoscendo un FUOCO e un PUNTO per il quale passa l'iperbole
Esempio:
scrivere l'equazione dell'iperbole riferita ai suoi assi, sapendo che il fuoco F1 ha coordinate (2;0) e che l'iperbole passa per il punto P(-2;3).
Innanzitutto sappiamo che
F1 (2;0).
Quindi il fuoco si trova sull'asse delle ascisse. E, di conseguenza, la nostra iperbole ha un'equazione del tipo:
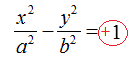
Ora dobbiamo trovare i valori di a2 e di b2.
Quando l'iperbole passa per il punto
P(-2;3)
essa assume i seguenti valori:

Inoltre conosciamo il valore di c che è pari a 2 e sappiamo che, la relazione che lega a, b, e c è la seguente:
b2 = c2 - a2
ovvero
-c2 = - b2 - a2
da cui
c2 = b2 + a2.
E poiché:
c = 2
possiamo scrivere:
4 = b2 + a2.
Ora mettiamo a sistema questa equazione con quella dell'iperbole passante per il punto P per trovare i valori di a e di b:

Poniamo
t = a2
z = b2.
Sostituiamo nel sistema e abbiamo:

Dalla seconda equazione ricaviamo il valore di t:

Sostituiamo, il valore di t appena trovato, nella prima equazione e andiamo a cercare il valore di z:

Applicando la formula risolutiva troviamo il valore di z:

Poiché abbiamo posto
z = b2
avremo:
b21 = -12
b22 = 3.
La prima soluzione non è accettabile poiché un quadrato non potrà mai essere un valore negativo. Rimane, dunque, la seconda soluzione. La sostituiamo nelle equazione
4 = b2 + a2
4 = 3 + a2
- a2 = 3 - 4
a2 = -3 + 4
a2 = 1.
L'equazione della nostra iperbole, dunque, è:

Riportiamo, di seguito, anche il grafico dell'iperbole:







