COME DISEGNARE UN'IPERBOLE
- L'iperbole
- Equazione dell'iperbole
- Elementi dell'iperbole
- Asintoti dell'iperbole
- Assi cartesiani ortogonali
In questa lezione cercheremo di capire come fare per disegnare un'IPERBOLE.
Lo faremo ricorrendo ad un esempio.
Supponiamo di voler disegnare l'iperbole di equazione
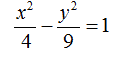
Noi sappiamo che:
a2 = 4
b2 = 9.
Di conseguenza
a = 2
b = 3.
Noi sappiamo che i vertici hanno coordinate
V1 (-a; 0)
V2 (a; 0)
Nel nostro caso, quindi, essi saranno:
V1 (-2; 0)
V2 (2; 0).
Li disegniamo sugli assi cartesiani:
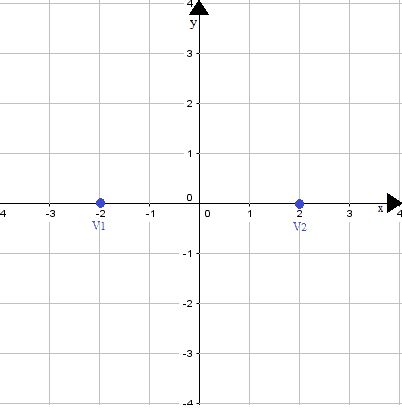
Essi rappresentano i PUNTI DI INTERSEZIONE DELL'IPERBOLE con l'ASSE delle x.
Inoltre sappiamo che gli ASINTOTI dell'iperbole passano per il centro e, una per il punto
N (a; b)
l'altra per il punto
N1 (a; -b).
Quindi, nel nostro caso un asintoto passa per il punto
N (2; 3)
e l'altro per il punto
N1 (2; -3).
Quindi disegniamo tali punti sugli assi cartesiani e tracciamo le rette passanti per essi e per il centro degli assi:
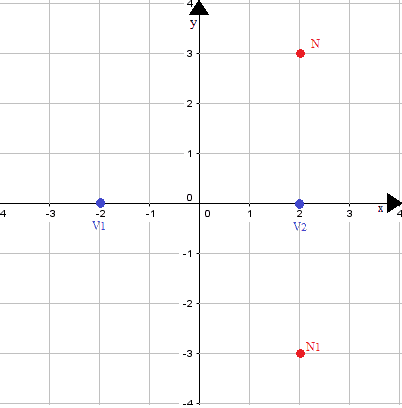
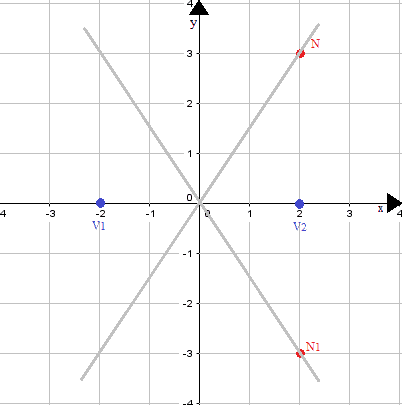
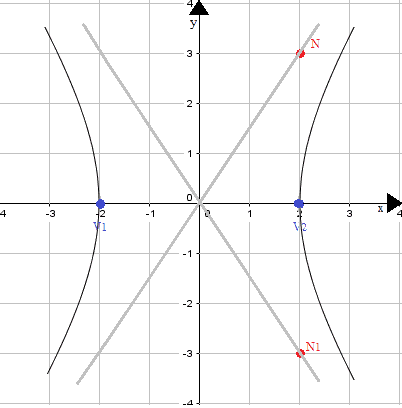
A questo punto disegniamo la curva sapendo che essa:
- interseca l'asse delle x nei punti V1 e V2;
- è simmetrica rispetto all'asse delle x e all'asse delle y;
- l'iperbole si avvicina agli asintoti senza mai toccarli.
Avremo: