EQUAZIONE DELL'IPERBOLE PASSANTE PER DUE PUNTI
- L'iperbole
- Equazione dell'iperbole
- Elementi dell'iperbole
- Asintoti dell'iperbole
- Proprietà dell'iperbole
- Come disegnare un'iperbole
- Eccentricità dell'iperbole
- Iperbole con fuochi sull'asse delle y
- Elementi dell'iperbole con fuochi sull'asse delle y
- Sistemi di equazioni di secondo grado
In questa lezione vedremo come è possibile scrivere l'EQUAZIONE DELL'IPERBOLE nel caso in cui conosciamo le coordinate di DUE PUNTI per i quali essa passa.
Esempio:
scrivere l'equazione dell'iperbole riferita ai suoi assi, avente i fuochi sull'asse delle ordinate e passante per i punti di coordinate
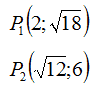
Innanzitutto sappiamo che i fuochi si trovano sull'asse delle ordinate. Questo significa che l'equazione da noi cercata è del tipo:
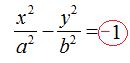
Ora dobbiamo trovare i valori di a2 e di b2.
Quando l'iperbole passa per il punto
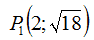
essa assume i seguenti valori:
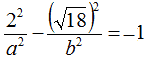
ovvero
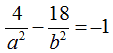
Quando l'iperbole passa per il punto
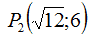
essa assume i seguenti valori:
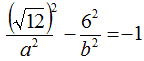
ovvero
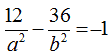
Per trovare i valori di a2 e di b2 mettiamo a sistema le due equazioni appena scritte, e avremo:
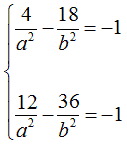
A questo punto si tratta di risolvere il sistema. Per farlo poniamo:
1/a2 = t
1/b2 = z.
Sostituiamo nel sistema e abbiamo:
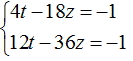
Dalla prima equazione ricaviamo il valore di t:
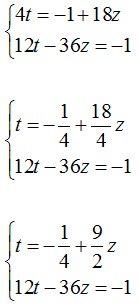
Sostituiamo, il valore di t appena trovato, nella seconda equazione:
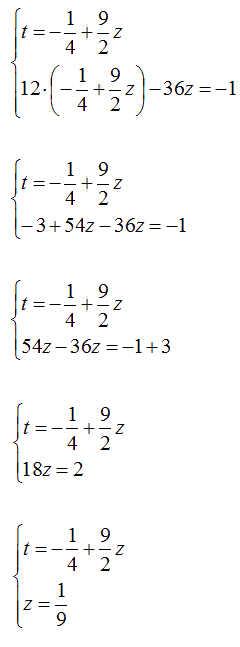
Sostituiamo, il valore di z appena trovato, nella prima equazione:
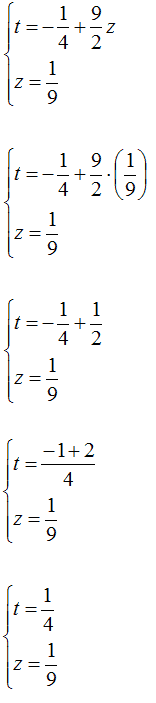
Poiché abbiamo posto
1/a2 = t
1/b2 = z
possiamo scrivere:
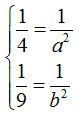
Quindi:
a2 = 4
b2 = 9.
Pertanto l'equazione da noi cercata è:
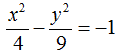
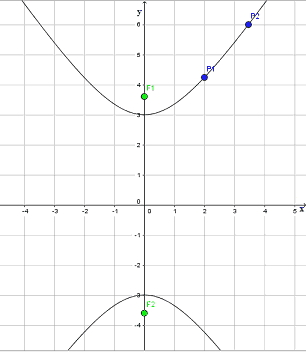
Riportiamo, di seguito, anche il grafico dell'iperbole: