POSIZIONE DI UNA RETTA RISPETTO ALL'IPERBOLE
- L'iperbole
- Equazione dell'iperbole
- Equazione della retta
- Sistemi di equazioni di secondo grado
- Risoluzione delle equazioni di secondo grado complete
- Rette parallele
Supponiamo di avere l'IPERBOLE di equazione
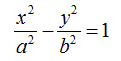
e supponiamo di avere la RETTA di equazione.
y = mx + n.
Ora ci chiediamo se esistono dei PUNTI di INTERSEZIONE tra l'iperbole e la retta.
Per rispondere alla nostra domanda dobbiamo mettere a sistema l'equazione dell'iperbole con quella della retta e cercare quei punti, se ci sono, che sono comuni ad entrambi. Quindi avremo:

Per risolvere il sistema è necessario sostituire l'equazione della retta in quella dell'iperbole.
In questo modo si otterrà un'EQUAZIONE DI SECONDO GRADO ad un'incognita (la x) che si risolve applicando la formula
In questo modo si potranno verificare due situazioni diverse:
- l'equazione
risolvente è di SECONDO GRADO.
In questo caso si possono avere tre casi diversi:
- La RETTA
è ESTERNA rispetto all'IPERBOLE.
La retta e l'iperbole non si incontrano in nessun punto, quindi non hanno nessun punto in comune.
Questo caso si verifica quando, il sistema visto sopra, non ammette soluzioni, cioè quando il DISCRIMINANTE della formula risolutiva è negativo.
Δ < 0

- La RETTA
è TANGENTE rispetto all'IPERBOLE
In altre parole la retta e l'iperbole hanno un solo punto in comune.
Questo caso si verifica quando, il sistema visto sopra, ammette una sola soluzione,cioè quando il DISCRIMINANTE della formula risolutiva è uguale a zero.
Δ = 0

In questo caso, una volta trovato il valore della x con la formula risolutiva, basta sostituirlo nell'equazione della retta per avere anche il valore della y.
I valori della x e della y trovati sono le coordinate del punto di intersezione P.
-
La RETTA
è SECANTE rispetto all'IPERBOLE
in DUE PUNTI.
In altre parole la retta e l'iperbole hanno due punti in comune.
Questo caso si verifica quando, il sistema visto sopra, ammette due soluzioni, cioè quando il DISCRIMINANTE della formula risolutiva è maggiore di zero.
Δ > 0

In questo caso, una volta trovati i valori x1 e x2 con la formula risolutiva, basta sostituirli nell'equazione della retta per avere anche il valore di y1 e di y2.
Le coordinate dei due punti di intersezione saranno
P1(x1 ; y2)
P2(x2 ; y2).
- La RETTA
è ESTERNA rispetto all'IPERBOLE.
- l'equazione
risolvente è di PRIMO GRADO.
In questo caso vi è una sola soluzione:

La RETTA è SECANTE rispetto all'IPERBOLE in UN SOLO PUNTO
In altre parole la retta e l'iperbole hanno un solo punto in comune.
La retta sarà, in questo caso, PARALLELA ad uno degli ASINTOTI.
Esempio:
determinare i punti di intersezione, se esistono, tra la retta di equazione
y = x - 3
e l'iperbole di equazione

Mettiamo a sistema l'equazione dell'iperbole e quella della retta:

Sostituiamo la seconda equazione nella prima e risolviamo:

Andiamo a vedere il valore assunto dal discriminante della prima equazione:
Δ = b2- 4ac
Δ = (-902)- 4 · 9 · 225 = 8100 - 8100 = 0.
Poiché
Δ = 0
il sistema ammette una sola soluzione, il che significa che la retta ètangente all'iperbole.
Ora andiamo a cercare il punto di intersezione. Troviamo l'ascissa di tale punto

L'ascissa del punto da noi cercato è 5.
Ora sostituiamo all'equazione della retta il valore di x appena trovato in modo da determinare il valore dell'ordinata:
y = x - 3
y = 5 - 3
y = 2.
L'ordinata del nostro punto è 2.
Quindi il punto di tangenza tra la retta e l'iperbole è
P (5; 2).






