EQUAZIONE DELLA CIRCONFERENZA CON CENTRO NELL'ORIGINE DEGLI ASSI
- Equazione della circonferenza
- Equazione della circonferenza: alcune considerazioni
- Equazione della circonferenza con centro sull'asse delle y
- Equazione della circonferenza con centro sull'asse delle x
- Equazione della circonferenza passante per l'origine degli assi
- Equazione della circonferenza con centro sull'asse delle y e passante per l'origine degli assi
- Equazione della circonferenza con centro sull'asse delle x e passante per l'origine degli assi
- Equazione della circonferenza: casi particolari
Concludiamo l'esame dell'equazione della circonferenza in casi particolari, parlando dell'ipotesi in cui la CIRCONFERENZA ha CENTRO nell'ORIGINE degli assi.
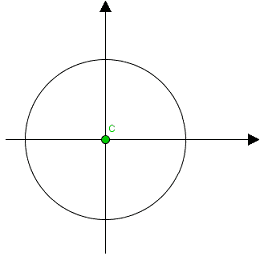
Per comprendere come si presenta l'equazione della circonferenza in questo caso dobbiamo ricordare che
- l'equazione
della circonferenza è
x2 + y2 + ax + by + c = 0
- che il
centro ha coordinate
C (α; β)
- e che
le relazioni che legano α e
β rispettivamente
ad a
e b
sono
-2α = a
e
-2β = b.
Quando la circonferenza ha CENTRO nell'ORIGINE degli assi essa ha coordinate
C (0; 0)
quindi
-2·0 = a
a = 0
e
-2·0 = b
b = 0.
Di conseguenza, l'equazione della circonferenza diventa
x2 + y2 + c = 0.
Inoltre, noi sappiamo che
α2 + β2 - r2 = c.
Ma poiché
α = 0
β = 0
Possiamo dire che
- r2 = c.
Quindi, l'equazione della circonferenza con origine nel centro degli assi cartesiani, può essere scritta anche nel modo che segue:
x2 + y2 - r2 = 0
che equivale a dire:
x2 + y2 = r2.






