RETTA PARALLELA ALL'ASSE DELLE Y
- Retta parallela all'asse delle x
- Rappresentazione di un punto su un pianto cartesiano
- Il punto
- Assi cartesiani ortogonali
- Costanti e variabili
Nella lezione precedente abbiamo visto qual'è l'equazione di una retta parallela all'asse delle x. Ora ci poniamo l'obiettivo di individuare l'EQUAZIONE della RETTA PARALLELA all'asse delle y.
Disegniamo sugli ASSI CARTESIANI il PUNTO
P (8; 0)
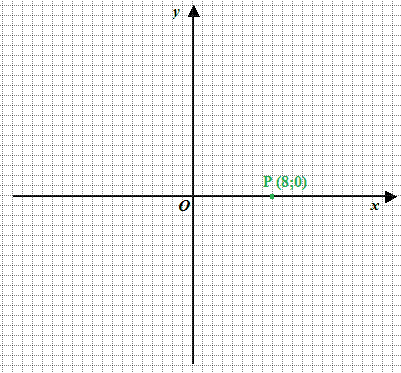
Ora disegniamo una RETTA PARALLELA all'asse delle y che intersechi l'asse delle x nel punto P:
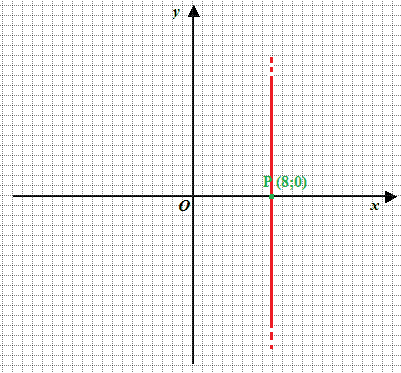
Individuiamo dei punti qualsiasi sulla retta che abbiamo appena disegnato Q, R, S, T, ecc...
E' evidente che essi HANNO TUTTI come ASCISSA 8:
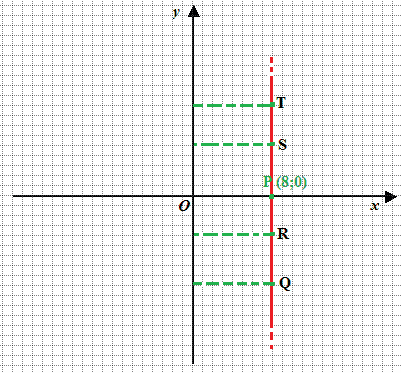
Di conseguenza possiamo affermare che la retta che abbiamo disegnato ha equazione
x = 8.
Generalizzando possiamo affermare che una RETTA PARALLELA all'asse delle y ha per equazione:
x = k.
Dove
k è una COSTANTE
e rappresenta l'ASCISSA del PUNTO in cui la RETTA INTERSECA l'asse delle x, ovvero:
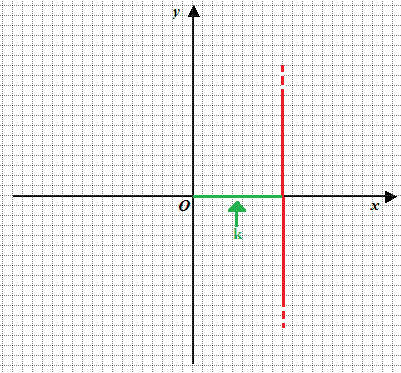
Quando
k = 0
si avrà
x = 0
che non è altro che l'EQUAZIONE DELL'ASSE DELLE y.






