COME TROVARE LA FUNZIONE INVERSA DI UNA FUNZIONE?
- Funzioni inverse
- Funzione invertibile in un intervallo
- Funzione invertibile e monotona
- Funzioni iniettive
- Come riconoscere se una funzione è iniettiva
- Come capire se una funzione è iniettiva
- Funzioni suriettive
- Come riconoscere se una funzione è suriettiva
- Funzioni biunivoche
- Come riconoscere se una funzione è biunivoca
- Equazione della retta
- Bisettrice del primo e terzo quadrante
Dopo aver visto quando una FUNZIONEè INVERTIBILE e cosa si intende per FUNZIONE INVERSA, ora ci chiediamo: "Data una funzione y = f(x) come faccio a trovare la sua inversa?"
Ecco le regole da seguire.
Data la funzione
y = f(x)
per trovare la sua inversa
x = f-1(y)
dobbiamo procedere nel modo seguente:
1 - per prima cosa dobbiamo vedere se la funzione è INVERTIBILE. Quindi verifichiamo che la funzione sia BIUNIVOCA. Se essa lo è allora si potrà trovare la funzione inversa;
2 - se la funzione non è biunivoca, andiamo a vedere se essa è INIETTIVA. Se la funzione è iniettiva (ma non suriettiva dato che essa non è biunivoca) allora la funzione è INVERTIBILE a condizione che noi RESTRINGIAMO L'IMMAGINE ad un intervallo opportuno;
3 - se la funzione NON è INIETTIVA essa NON è neppure INVERTIBILE e dunque non possiamo trovare l'inversa della funzione data;
4 - se la funzione y = f(x) è INVERTIBILE passiamo a trovare la sua inversa. Attraverso opportuni passaggi algebrici occorre passare da una funzione dove la x è la variabile indipendente e la y la variabile dipendente ad una funzione nella quale la y è la variabile indipendente e la x è la variabile dipendente.
Esempio:
y = x + 8.
Disegniamo la nostra funzione
| x | y |
|---|---|
| 0 | 8 |
| 1 | 9 |
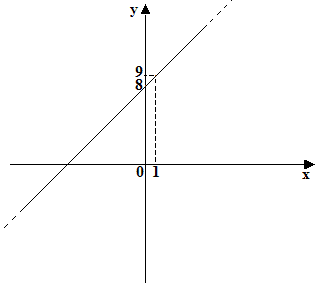
La funzione disegnata è una retta: essa è biunivoca. Quindi è invertibile.
Troviamo, allora, la funzione inversa.
Per fare ciò scambiamo nella funzione f la x con la y. Partiamo dalla funzione f:
y = x + 8.
Scambiamo la x con la y:
x = y + 8.
Ora esplicitiamo in funzione della y, cioè portiamo la y a primo membro cambiando di segno e portiamo la x a secondo membro cambiando di segno:
- y = - x + 8.
Cambiamo di segno ad entrambi i membri:
y = x - 8.
Abbiamo così ottenuto la nostra funzione inversa. Ora andiamo a disegnarla:
| x | y |
|---|---|
| 0 | -8 |
| 1 | -7 |
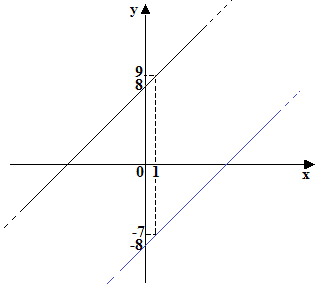
La funzione disegnata in azzurro è la funzione inversa.
Ora osserviamo il grafico della funzione inversa f-1: esso è SIMMETRICO del grafico di f rispetto alla bisettrice del 1° e del 3° quadrante che, nell'immagine sottostante abbiamo indicato in rosso.
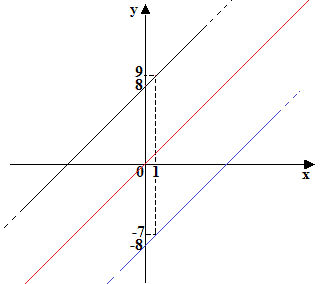
Tale simmetria esiste per qualsiasi funzione inversa.
Nella prossima lezione vedremo altri esempi di funzioni inverse.






