FUNZIONI INIETTIVE
- Funzioni reali di variabile reale
- Come riconoscere se una funzione è iniettiva
- Come capire se una funzione è iniettiva
- Funzioni suriettive
- Come riconoscere se una funzione è suriettiva
- Funzioni biunivoche
- Come riconoscere se una funzione è biunivoca
- Nozione di insieme
- Implicazione logica
- Rappresentazione grafica di un insieme
Consideriamo la funzione
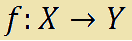
che si legge
f di X in Y.
Essa associa, mediante la relazione f, ad ogni elemento x appartenente all'insieme X, un solo elemento y appartenente all'insieme Y.
Se, ad ELEMENTI DIVERSI di X corrispondono ELEMENTI DIVERSI di Y, la FUNZIONE si dice INIETTIVA.
In altre parole, dati
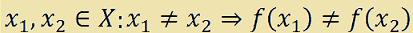
che si legge
x con 1 e x con 2 appartenenti all'insieme X tali che x con 1 è diverso da x con 2 implica che f con x con 1 è diverso da f con x con 2.
Graficamente possiamo rappresentare una FUNZIONE INIETTIVA con i seguenti diagrammi di Venn:
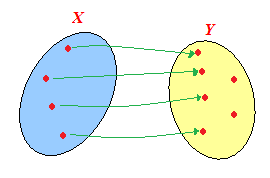
Come possiamo notare ad ELEMENTI DIVERSI dell'insieme X corrispondono ELEMENTI DIVERSI dell'insieme Y. Osserviamo, però, che ci sono elementi dell'insieme Y che non sono raggiunti da nessuna freccia.
Di seguito riportiamo il grafico di due funzioni: la prima è iniettiva, mentre la seconda non lo è.
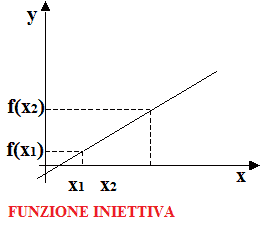
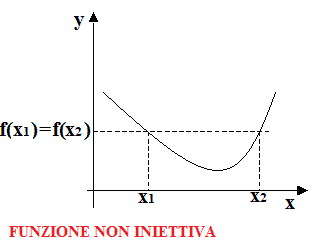
Nella prossima lezione vedremo come riconoscere se una funzione è iniettiva o no.






