COME RICONOSCERE SE UNA FUNZIONE E' INIETTIVA
- Funzioni reali di variabile reale
- Funzioni iniettive
- Come capire se una funzione è iniettiva
- Funzioni suriettive
- Come riconoscere se una funzione è suriettiva
- Funzioni biunivoche
- Come riconoscere se una funzione è biunivoca
- Rette parallele
Nella lezione precedente abbiamo detto che una FUNZIONE è INIETTIVA se ad ELEMENTI DIVERSI di X corrispondono ELEMENTI DIVERSI di Y.
Ora, vogliamo vedere come è possibile, una volta disegnata graficamente una funzione, stabilire se essa è INIETTIVA o meno.
Esempio:
data la funzione disegnata sotto vogliamo sapere se essa è iniettiva.
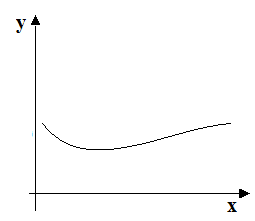
Per stabilire se la nostra FUNZIONE è INIETTIVA o meno useremo il cosiddetto TEST DELLE RETTE ORIZZONTALI. Vediamo in cosa consiste.
Si tratta di TRACCIARE delle RETTE PARALLELE all'ASSE DELLE ASCISSE.
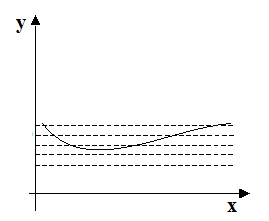
Se almeno una delle rette tracciate, INTERSECA IL GRAFICO in ALMENO DUE PUNTI DISTINTI, la funzione NON E' INIETTIVA dato che ad elementi distinti di X non corrispondono elementi distinti di Y.
Ad esempio, la funzione da noi disegnata non è iniettiva poiché le rette parallele all'asse delle x che abbiamo disegnato intersecano la funzione in due punti distinti:
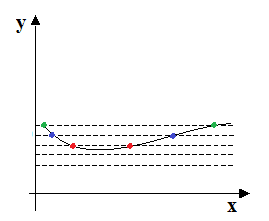
I due punti evidenziati in rosso rappresentano due valori distinti di X a cui viene associato uno stesso valore di Y.
La stessa cosa possiamo dire per i due punti evidenziati in azzurro e per i due punti evidenziati in verde.
Esiste anche un altro metodo per comprendere se una funzione è iniettiva e lo vedremo nella prossima lezione.






