FUNZIONI BIUNIVOCHE
- Funzioni reali di variabile reale
- Funzioni iniettive
- Come riconoscere se una funzione è iniettiva
- Come capire se una funzione è iniettiva
- Funzioni suriettive
- Come riconoscere se una funzione è suriettiva
- Come riconoscere se una funzione è biunivoca
- Nozione di insieme
- Rappresentazione grafica di un insieme
Esaminiamo la funzione
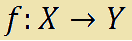
che si legge
f di X in Y.
Essa fa corrispondere, mediante la relazione f, ad ogni elemento x appartenente all'insieme X, uno e un solo elemento y appartenente all'insieme Y.
Se la funzione da noi considerata è, al tempo stesso, sia INIETTIVA che SURIETTIVA, la funzione si dice BIIETTIVA o BIUNIVOCA.
Come abbiamo visto nelle precedenti lezioni, una funzione si dice:
- INIETTIVA, se ad elementi diversi di X corrispondono elementi diversi di Y;
- SURIETTIVA se, ogni elemento di Y è immagine di almeno un elemento di X.
Quindi, una funzione è BIUNIVOCA se ogni elemento di Y è immagine di uno e un solo elemento di X.
Graficamente possiamo rappresentare una FUNZIONE BIUNIVOCA coi diagrammi di Venn, nel modo seguente:
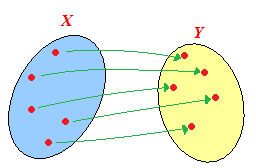
Notiamo:
- ad elementi distinti di X corrispondono elementi distinti di Y;
- tutti gli elementi di Y sono immagine di almeno un elemento diX.
Di seguito riportiamo il grafico di una funzione biunivoca:
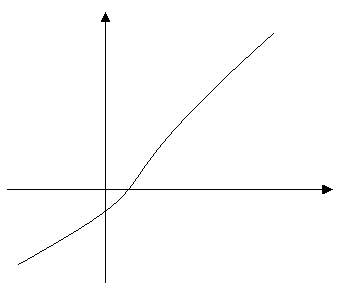
E' evidente che, nella funzione disegnata:
- ad elementi distinti di X corrispondono elementi distinti di Y;
- tutti gli elementi di Y sono immagine di almeno un elemento diX.
Nella prossima lezione vedremo come riconoscere se una funzione è biunivoca.






