FUNZIONI SURIETTIVE
- Funzioni reali di variabile reale
- Funzioni iniettive
- Come riconoscere se una funzione è iniettiva
- Come capire se una funzione è iniettiva
- Come riconoscere se una funzione è suriettiva
- Funzioni biunivoche
- Come riconoscere se una funzione è biunivoca
- Nozione di insieme
- Rappresentazione grafica di un insieme
- Bisettrice del primo e terzo quadrante
Sia data la funzione
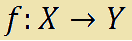
che si legge
f di X in Y.
Come sappiamo tale funzione fa corrispondere, mediante la relazione f, ad ogni elemento x appartenente all'insieme X, un solo elemento y appartenente all'insieme Y.
Se, OGNI ELEMENTO di Y è IMMAGINE di ALMENO UN ELEMENTO di X la FUNZIONE si dice SURIETTIVA.
Quindi, una funzione è SURIETTIVA, se

che si legge
per qualunque y appartenente all'insieme Y esiste una x appartenente all'insieme X tale che f con x è uguale ad y.
Graficamente possiamo rappresentare una FUNZIONE SURIETTIVA con i seguenti diagrammi di Venn:

Notiamo che tutti gli elementi di Y sono immagine di almeno un elementoX. Osserviamo, però, che si sono elementi dell'insieme Y che sono raggiunti da due frecce perché associati a due elementi dell'insieme X.
Di seguito riportiamo il grafico di una funzione suriettiva:

Quella che abbiamo disegnato è la bisettrice del 1° e del 3° quadrante.
E' evidente che, nella funzione disegnata tutti gli elementi di Y sono immagine di almeno un elementoX.
Nella prossima lezione vedremo come riconoscere se una funzione è suriettiva o meno.






