FUNZIONE INVERTIBILE E MONOTONA
- Funzioni reali di variabile reale
- Funzioni inverse
- Funzioni monotone
- Monotonia generale e monotonia locale
- Funzioni iniettive
- Come riconoscere se una funzione è iniettiva
- Come capire se una funzione è iniettiva
- Implicazione logica
Consideriamo la seguente la funzione
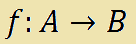
e supponiamo che tale funzione sia STRETTAMENTE MONOTÒNA.
Ciò significa che, dati due valori x1 e x2 appartenenti al suo CAMPO DI ESISTENZA possiamo dire che:
- se x1 è minore di x2 avremo che f(x1) è minore di f(x2)
- se x1 è minore di x2 avremo che f(x1) è maggiore di f(x2).
Nel primo caso la funzione è STRETTAMENTE CRESCENTE, mentre nel secondo caso essa è STRETTAMENTE DECRESCENTE.
Quindi, in entrambi i casi possiamo dire che, in una funzione STRETTAMENTE MONOTÒNA si avrà che:

che si legge
x con 1 diverso da x con 2 implica che f di x con 1 è diverso da f di x con 2.
Ma questo significa affermare che la funzione è INIETTIVA e dunque, essa è INVERTIBILE.
Abbiamo, quindi, dimostrato che una FUNZIONE STRETTAMENTE MONOTÒNA è una FUNZIONE INVERTIBILE.
Tuttavia una funzione può essere invertibile anche se non è strettamente monotona.
Esempio:

La funzione disegnata non è una funzione strettamente monotòna, ma è una funzione invertibile.
Ora torniamo alla nostra funzione strettamente monotòna e chiamiamo con f-1 la sua funzione inversa. Vogliamo verificare che anche quest'ultima sia strettamente monotòna.
Partiamo dal caso in cui la funzione f sia crescente. Ovvero:
x1 < x2
e di conseguenza
f(x1) < f(x2)
che potremmo scrivere anche come
y1 < y2.
Ora prendiamo la funzione inversa f-1 e consideriamo il caso in cui
y1 < y2
non potrà essere che
x1 > x2
né che
x1 = x2
dato che in partenza abbiamo posto che
x1 < x2.
Quindi anche la funzione f-1 sarà strettamente crescente.
Potremmo fare le stesse considerazioni partendo da una funzione strettamente decrescente.
Quindi concludendo possiamo dire che una FUNZIONE STRETTAMENTE MONOTÒNA è una FUNZIONE INVERTIBILE e la FUNZIONE INVERSA è anch'essa una FUNZIONE STRETTAMENTE MONOTÒNA.






