RISOLUZIONE DI DISEQUAZIONI ESPONENZIALI CON METODO GRAFICO
- Funzione esponenziale
- I logaritmi: definizione
- Logaritmi: casi particolari
- Teoremi sui logaritmi: teorema della potenza di un logaritmo
- Disequazioni esponenziali
- Disequazioni esponenziali con potenze aventi la stessa base
- Disequazioni esponenziali con potenze aventi lo stesso esponente
- Disequazioni esponenziali con potenze aventi basi ed esponenti diversi
- Disequazioni esponenziali con una potenza ed una costante
- Risoluzione di disequazioni esponenziali mediante sostituzione
- Risoluzione di disequazioni esponenziali con metodo grafico
- Risoluzione delle equazioni di secondo grado complete
Finora ci siamo occupati di DISEQUAZIONI nelle quali l'INCOGNITA compare solamente ad ESPONENTE. Ma cosa accade se l'incognita è presente non solamente nell'esponente.
Supponiamo di trovarci di fronte ad una disequazione che assume una delle forme seguenti:
af(x) > g(x)
af(x) < g(x)
af(x) ≥ g(x)
af(x) ≤ g(x).
In questi casi, l'unico modo che abbiamo per risolvere la disequazione è usare il METODO GRAFICO.
Va precisato che, con questo metodo, non otteniamo un risultato esatto.
Vediamo come occorre procedere.
Innanzitutto, se la disequazione non si presenta in una delle forme appena viste, che chiameremo FORMA NORMALE, dobbiamo ricondurla ad una di esse eseguendo le opportune operazioni.
Subito dopo occorre DISEGNARE i GRAFICI delle due funzioni:
y = af(x)
e
y' = gf(x).
A questo punto bisogna esaminare il SEGNO DELLA FUNZIONE:
- se il segno è MAGGIORE (>) le soluzioni sono date dalle x tali che la funzione y si trova al di sopra della funzione y';
- se il segno è MINORE <) x tali che la funzione y si trova al di sotto della funzione y'.
Ovviamente, se il segno della disequazione è MAGGIORE UGUALE (≥) o MINORE UGUALE (≤) nella soluzione includeremo gli estremi, altrimenti no.
Vediamo, con alcuni esempi, come procedere.
Esempio:
(1/5)x > -x2 + 3.
La prima cosa da fare è disegnare i grafici delle due funzioni
y = (1/5)x
y' = -x2 + 3.
Lo facciamo attribuendo alcuni valori alla x e cercando i corrispondenti valori delle y:
y = (1/5)x
| x | y |
|---|---|
| -1 | 5 |
| 0 | 1 |
| 1 | 1/5 |
| 2 | 1/25 |
y' = -x2 + 3
| x | y |
|---|---|
| -2 | -1 |
| -1 | 2 |
| 0 | 3 |
| 1 | 2 |
| 2 | -1 |
Il grafico delle due funzioni è il seguente.
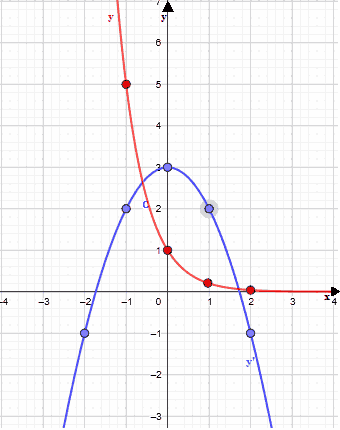
Ora, dato che il segno della nostra disequazione è MAGGIORE, le soluzioni sono date dai valori delle x tali che
y
> y'.
In pratica le soluzioni sono individuate dalla parte di grafico che abbiamo tratteggiato di verde:
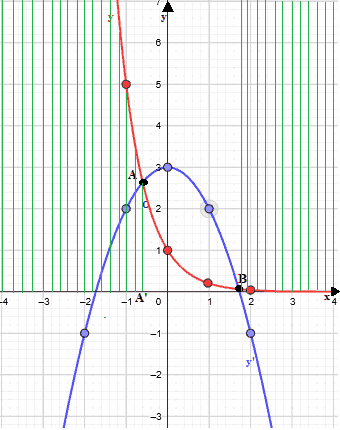
Quindi la soluzione sarà data dalle
x < A'
e
x
> B.
Se la nostra disequazione fosse stata
(1/5)x ≥ -x2 + 3
nelle soluzioni avremmo dovuto includere anche i punti A' e B, cioè:
x A'
e
x
≥
B.
Se la disequazione fosse stata
(1/5)x < -x2 + 3
le soluzioni sarebbero state date dai valori delle x tali che
y < y'
cioè:
A'
< x < B.
Infine se la disequazione fosse stata
(1/5)x ≤ -x2 + 3
le soluzioni sarebbero state
A' ≤ x ≤ B.






