DISTANZA DI UNA RETTA DALL'ORIGINE DEGLI ASSI
- Equazione della retta
- Rappresentazione grafica di una funzione
- Punti di intersezione di una retta con gli assi cartesiani
- Punto di intersezione tra due rette
- Il segmento
- Triangolo rettangolo
- Rette perpendicolari
- Angolo retto - angolo acuto - angolo ottuso
- Altezze di un triangolo
- Area del triangolo
- I numeri relativi
- Moltiplicazione di numeri relativi
- Le formule del teorema di Pitagora
- Raccoglimento a fattor comune
Scriviamo l'equazione della retta
ax + by + c = 0
e andiamo a disegnarla:

Indichiamo con A e B i PUNTI in cui essa INTERSECA gli ASSI CARTESIANI.

Ora vogliamo sapere qual è la DISTANZA della RETTA dall'ORIGINE degli assi. Tale distanza è individuata, nell'immagine sottostante, dal segmento OH:

Cerchiamo di capire come possiamo trovare la misura di tale segmento.
Notiamo che OBA non è altro che un TRIANGOLO RETTANGOLO.
Osserviamo che, qualunque sia l'inclinazione della retta, il triangolo che si ottiene è sempre rettangolo poiché gli assi cartesiani sono tra loro perpendicolari e, dunque, l'angolo O è un angolo retto.
OH non è altro che l'ALTEZZA del triangolo RELATIVA ALL'IPOTENUSA.
Iniziamo col trovare i PUNTI DI INTERSEZIONE della nostra retta con gli ASSI CARTESIANI. Lo facciamo risolvendo i due sistemi:

Risolviamo il primo sistema:
Sostituiamo il valore della y nella prima equazione e otteniamo:
ax + b · 0 + c = 0
ax + c = 0
x = -c/a.
Abbiamo così trovato il punto A di intersezione con l'asse delle x. Esso è:
A (-c/a ; 0).
Ora risolviamo il secondo sistema. Sostituiamo il valore della x nella prima equazione e otteniamo:
a · x + by + c = 0
by + c = 0
y = -c/b.
Abbiamo così trovato il punto B di intersezione con l'asse delle y. Esso è:
B (0 ; -c/a).
A questo punto andiamo a calcolare l'AREA DEL TRIANGOLO. Sappiamo che essa è data da base per altezza e prodotto diviso due, ovvero:
A = (OA · OB)/ 2.
Ma noi sappiamo che:
OA = -c/a
OB = -c/b
quindi possiamo scrivere:

Poiché l'area di una figura geometrica è sempre un valore positivo, dobbiamo prendere il valore assoluto del prodotto sopra indicato, ovvero:

Risolviamo e abbiamo:

Ora notiamo che:
- c2 è sempre positivo trattandosi del prodotto di un numero per se stesso (e dalla regola dei segni sappiamo che il prodotto di due segni concordi è sempre positivo);
- 2 è un numero positivo;
quindi affinché A sia positivo è sufficiente che sia positivo il prodotto tra a e b. Quindi possiamo scrivere:

Ora andiamo a trovarci l'IPOTENUSA applicando il TEOREMA DI PITAGORA. Ovvero:

Sostituiamo e abbiamo:

Ma poiché un numero al quadrato è sempre positivo, possiamo scrivere:

Eseguiamo i calcoli:

A numeratore mettiamo in evidenza la c:

Ora estraiamo la radice quadrata di c2 e di a2b2 e poniamo le sbarre di valore assoluto sempre affinché il segmento cercato sia un valore positivo:

Ora conosciamo l'area del triangolo e l'ipotenusa. Applicando la formula inversa dell'area sappiamo che l'altezza (in questo caso relativa all'ipotenusa) è data dal rapporto tra doppia area e ipotenusa. Ovvero:

Andiamo a sostituire i valori precedentemente ottenuti ed avremo:

Quindi, data la retta di equazione
ax + by + c = 0
la DISTANZA dell'ORIGINE da tale RETTA è
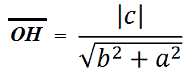
Nella prossima lezione vedremo come applicare tale formula a dei casi concreti.






