RAPPRESENTAZIONE GRAFICA DI UNA FUNZIONE
- Le funzioni
- Funzioni matematiche
- Assi cartesiani ortogonali
- Rappresentazione di un punto su un pianto cartesiano
- Perimetro dei quadrilateri
- Quadrato
- Nozione di insieme
Nella lezione precedente abbiamo parlato di FUNZIONI MATEMATICHE e abbiamo detto che una funzione è tale quando il legame che associa la variabile dipendente alla variabile indipendente può essere espresso da una formula.
Esempio:
la funzione che esprime il perimetro di un quadrato dato il suo lato è una funzione matematica.
Ricordiamo che il perimetro del quadrato si ottiene moltiplicando per 4 il suo lato. Quindi la nostra funzione è la seguente:
y = 4x.
L'INSIEME DEI NUMERI nel quale viene scelta la VARIABILE INDIPENDENTE x è detto DOMINIO.
L'insieme dei numeri al quale appartiene la VARIABILE DIPENDENTE y è detto CODOMINIO.
Ora vediamo come possiamo rappresentare la nostra funzione.
Costruiamo una tabella con due colonne e un certo numero variabile di righe.
Nella PRIMA COLONNA indicheremo i valori delle x.
Nella SECONDA COLONNA indicheremo i valori delle y.
| x | y |
|---|---|
Iniziamo a costruire la nostra tabella. Essendo la x la variabile indipendente saremo noi a scegliere quali valori vogliamo assegnare alla x. Mentre, per ciò che concerne la variabile y, dovremo andare a vedere quale valore essa assumerà dato un certo valore della x.
Cominciamo con l'assegnare alla x il valore 0. Scriviamo tale valore nella tabella nella colonna delle x:
| x | y |
|---|---|
| 0 | |
Se la x vale 0, quale sarà il valore della y?
Lo troviamo sostituendo, nella funzione, alla x il valore 0:
y = 4·0 = 0.
Quindi, quando la x vale 0, la y vale 0. Scriviamo tale valore nella tabella, nella colonna delle y in corrispondenza del valore 0 della x:
| x | y |
|---|---|
| 0 | 0 |
Scegliamo un altro valore da assegnare alla x, ad esempio il valore 1 e lo scriviamo nella tabella nella colonna delle x:
| x | y |
|---|---|
| 0 | 0 |
| 1 |
Se la x vale 1, quale sarà il valore della y?
Lo troviamo sempre sostituendo, nella funzione, alla x il valore 1:
y = 4·1 = 4.
Quindi, quando la x vale 1, la y vale 4. Scriviamo tale valore nella tabella, nella colonna delle y in corrispondenza del valore 1 della x:
| x | y |
|---|---|
| 0 | 0 |
| 1 | 4 |
Andiamo avanti.
Se la x vale 2, la y ha il valore di:
y = 4·2 = 8.
Scriviamo i due valori nella tabella:
| x | y |
|---|---|
| 0 | 0 |
| 1 | 4 |
| 2 | 8 |
Ora, ad esempio, diamo alla x il valore di 4. La y varrà::
y = 4·4 = 16.
Scriviamo anche questi valori nella tabella:
| x | y |
|---|---|
| 0 | 0 |
| 1 | 4 |
| 2 | 8 |
| 4 | 16 |
Adesso che abbiamo stabilito un certo numero di valori per la x e per la y andiamo a rappresentare la nostra funzione sugli ASSI CARTESIANI.
Disegniamo gli assi cartesiani:
Ora andiamo a rappresentare, i punti appena individuati, sul piano cartesiano.
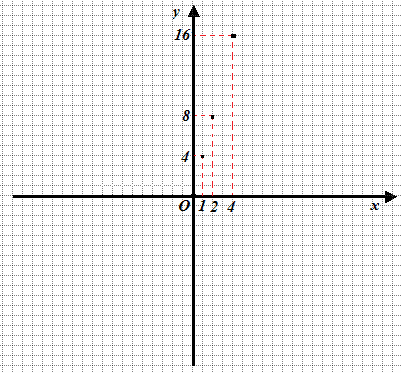
Adesso uniamo i punti individuati:
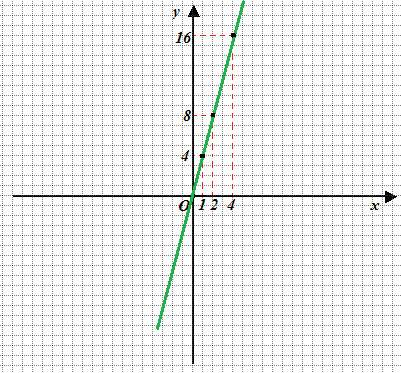
Quello che abbiamo ottenuto è il DIAGRAMMA CARTESIANO della nostra FUNZIONE.






