EQUAZIONE DELLA CIRCONFERENZA DATI IL CENTRO E IL RAGGIO
- Equazione della circonferenza
- Equazione della circonferenza: alcune considerazioni
- Quadrato di un binomio
In questa lezione cercheremo di capire come possiamo scrivere l'EQUAZIONE di una CIRCONFERENZA quando ci vengono dati:
- le coordinate del CENTRO;
- il RAGGIO.
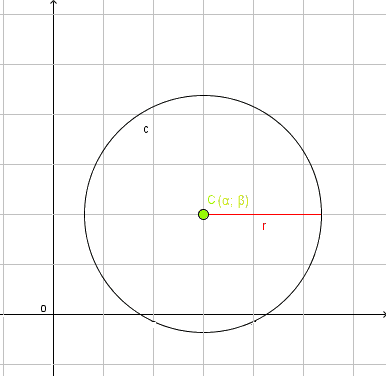
Si supponga che le coordinate del centro C siano
C (α; β)
e che r sia il raggio della circonferenza.
In questo caso è sufficiente usare la formula:
(x - α)2 + (y- β)2 = r2
e sostituire in essa i valori di α, β ed r.
Vediamo come fare concretamente con un esempio.
Esempio:
scrivere la circonferenza avente il centro C di coordinate (2; 3) e il raggio r = 5.
Partiamo dalla formula
(x - α)2 + (y - β)2 = r2.
Nel nostro caso sappiamo che
α = 2
β = 3
r = 5.
Sostituiamo nella formula precedente e avremo:
(x - 2)2 + (y - 3)2 = 52.
Eleviamo al quadrato applicando le regole relative al quadrato di un binomio e avremo:
x2 + 4 - 4x + y2 +9 - 6y = 25.
Portiamo a primo membro 25 e gli cambiamo di segno:
x2 + 4 - 4x + y2 + 9 - 6y - 25 = 0.
Sommiamo i termini simili:
x2 + 4 - 4x + y2 + 9 - 6y - 25 = 0
x2 - 4x + y2 - 6y - 12 = 0.
Ordiamo un po' i termini e scriviamo:
x2 + y2 - 4x - 6y - 12 = 0.
E abbiamo ottenuto l'equazione della nostra circonferenza.






