FASCIO DI RETTE PASSANTI PER UN PUNTO
- Fascio di rette passanti per un punto: esercizi
- Rappresentazione grafica di una funzione
- Bisettrice del primo e terzo quadrante
- Bisettrice del secondo e quarto quadrante
- Traslazione degli assi cartesiani
- Proprietà della retta
- Il punto
- La retta
Fissiamo un punto P0 sul piano tale che:
P0 (x0; y0)
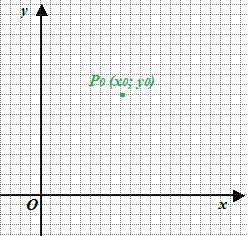
Dallo studio della geometria sappiamo che PER UN PUNTO PASSANO INFINITE RETTE. Quindi, per il punto P0 passano infinite rette.
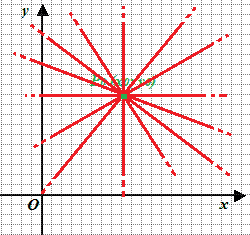
Si dice che esse formano un FASCIO di RETTE avente centro nel punto P0.
Se questo punto è l'ORIGINE degli assi, l'equazione di ogni retta passante per esso è data da:
y = mx.
A seconda del valore assunto da m avremo l'equazione di una particolare retta passante per l'origine degli assi.
Esempio:
m = 1
l'equazione diventa
y = x
che non è altro che la bisettrice del primo e terzo quadrante:
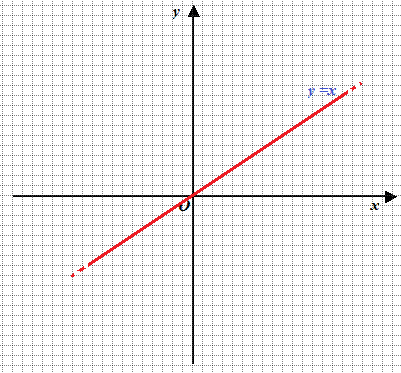
Ora poniamo
m = -1
l'equazione diventa
y = -x
che non è altro che la bisettrice del secondo e quarto quadrante:
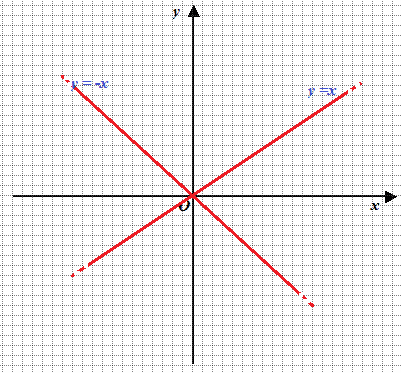
Poniamo
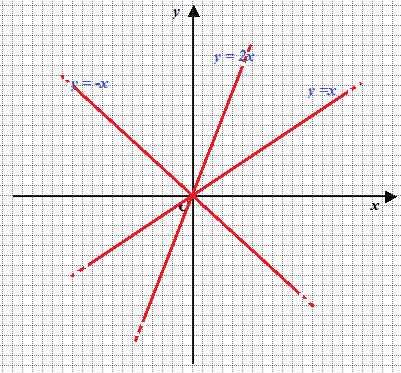
m = 2
l'equazione diventa
y = 2x.
La disegniamo:
E ancora
m = -2
y = -2x.
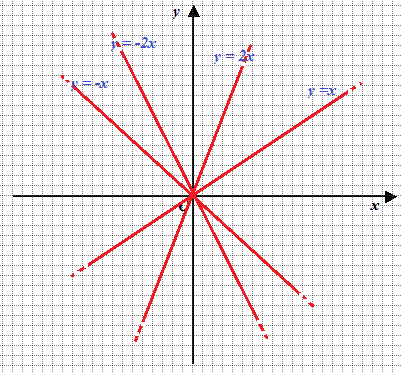
Potremmo andare avanti così per ogni possibile valore di m.
Diciamo allora che
y = mx
è l'EQUAZIONE DEL FASCIO di RETTE PASSANTI per l'ORIGINE.
E se ora volessimo scrivere l'equazione del fascio di rette passanti per il punto P0?
Possiamo effettuare una TRASLAZIONE degli assi che porti l'origine nel punto P0:
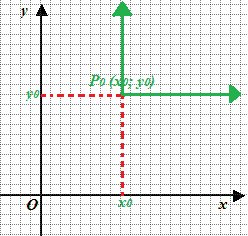
Ora chiamiamo x' e y' le coordinate del punto P0 sul nuovo sistema di assi cartesiani (quello in verde).
La relazione che lega le coordinate del punto P0 sul nuovo sistema di assi con quelle del precedente sistema di assi è la seguente:
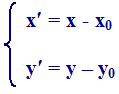
Quindi, se l'equazione della retta passante per l'origine, nel precedente sistema di assi cartesiani, era:
y = mx
nel nuovo sistema di assi cartesiani (quello in verde), sarà:
y - y0 = m (x - x0).
Quella che abbiamo scritto è l'EQUAZIONE GENERICA del FASCIO di RETTE PASSANTI per un PUNTO.
Nella prossima lezione vedremo alcune applicazioni pratiche.
Come abbiamo detto nel caso dell'equazione del fascio di rette passanti per l'origine, anche in questo caso, variando il valore assunto da m, varia la retta passante per il punto P0.
Esiste anche un altro modo per giungere a questa formula: ve lo spieghiamo negli approfondimenti, dove illustriamo anche le differenze tra le due formule.
- Fascio di rette passanti per un punto: una diversa dimostrazione della formula
- Fascio di rette passanti per un punto: alcune considerazioni






