EQUAZIONE DELLA RETTA PASSANTE PER DUE PUNTI
- Fascio di rette passanti per un punto
- Fascio di rette passanti per un punto: esercizi
- Retta passante per l'origine degli assi
- Coefficiente angolare
- Frazioni algebriche
- Equazione della retta passante per due punti: esercizi
Ora vogliamo capire come possiamo scrivere l'EQUAZIONE della RETTA passante per DUE PUNTI.
Immaginiamo di avere i punti
P0 (x0 ; y0) e P1 (x1 ; y1)
e di voler scrivere la retta passante per essi.
Iniziamo con lo scrivere il FASCIO di RETTE passanti per P0. Essa è
y - y0 = m (x - x0).
Assegnando ad m valori differenti potremo scrivere rette diverse, tutte passanti per P0, ma avente ognuna un'inclinazione diversa.
Ora noi stiamo cercando quella retta che, oltre a passare per P0, passa anche per P1. In altre parole, tra tutte le rette che passano per P0 vogliamo trovare quella retta che passa anche per P1. Ma, se un punto appartiene ad una retta, le sue coordinate ne verificano l’equazione: quindi, la retta passante anche per P1 sarà:
y1 - y0 = m (x1 - x0).
Ora cerchiamo il COEFFICIENTE ANGOLARE di questa retta. Lo possiamo ottenere dall'equazione precedente dividendo entrambi i membri per
x1 - x0.
Per fare questo, però, dobbiamo porre come condizione che
x1 ≠ x0
affinché l'equazione non perda di significato.
Posta questa condizione avremo che:
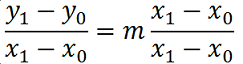
da cui otteniamo
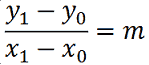
Quindi, il coefficiente angolare della retta passante sia per il punto P0 che per il punto P1 è:
m = (y1 - y0)/ (x1 - x0).
Ora torniamo all'equazione del fascio di rette passanti per il punto P0 e sostituiamo, in essa, il valore del coefficiente angolare appena trovato, avremo l'equazione della retta dell'inclinazione da noi cercata:
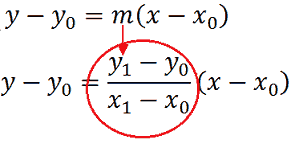
Ora ponendo come condizione
y1 ≠ y0
possiamo dividere ambo i membri per
y1 - y0
e avremo
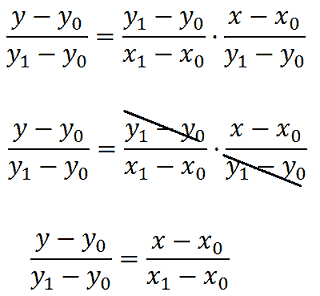
Dunque l'EQUAZIONE della RETTA passante per DUE PUNTI è:
(y - y0)/ (y1 - y0) = (x - x0)/ (x1 - x0).
Nella prossima lezione vedremo come applicare tale formula.






