PRODOTTO DI DUE SIMMETRIE ASSIALI CON ASSI PARALLELI
- Trasformazioni geometriche
- Simmetria assiale
- Figure simmetriche rispetto ad un asse
- Prodotto di due simmetrie assiali con assi incidenti
- Punti simmetrici rispetto ad una retta
Nella lezione precedente abbiamo parlando del prodotto di due
simmetrie assiali nel caso in cui gli assi siano incidenti. Ora esamineremo il caso in cui i due
ASSI DI SIMMETRIA siano
PARALLELI.
Disegniamo una figura piana F e la retta r che sarà il nostro ASSE DI SIMMETRIA.
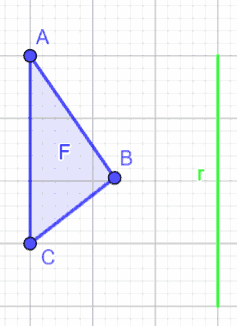
Costruiamo, come abbiamo già fatto nelle lezioni precedenti, la figura F' ad essa simmetrica rispetto all'asse di simmetria r.
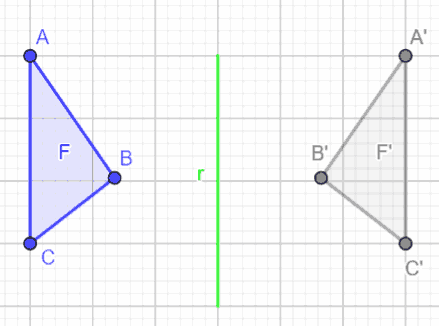
Ora disegniamo un'altra retta, che chiamiamo s che sia PARALLELA rispetto ad r.
e costruiamo la figura F'' simmetrica alla figura F' rispetto all'asse di simmetria s.
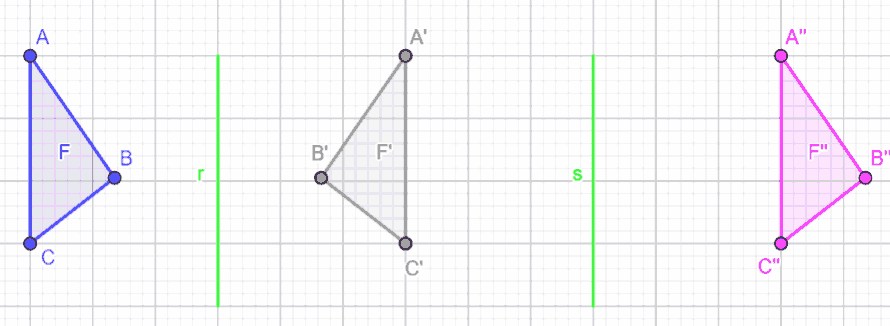
Anche in questo caso, così come abbiamo visto nella lezione precedente, diciamo che la figura F è stata trasformata nella figura F'' mediante il PRODOTTO delle due SIMMETRIE considerate.
Ora osserviamo la figura F e la figura F'': esattamente come accade nel caso del prodotto di due simmetrie assiali con assi incidenti, anche nel caso in cui i due assi di simmetria siano paralleli, le due figure NON SONO SIMMETRICHE tra loro.
E' abbastanza evidente osservare che saremmo potuti passare direttamente dalla figura
F alla figura F'' mediante una
TRASLAZIONE di
vettore
.
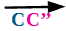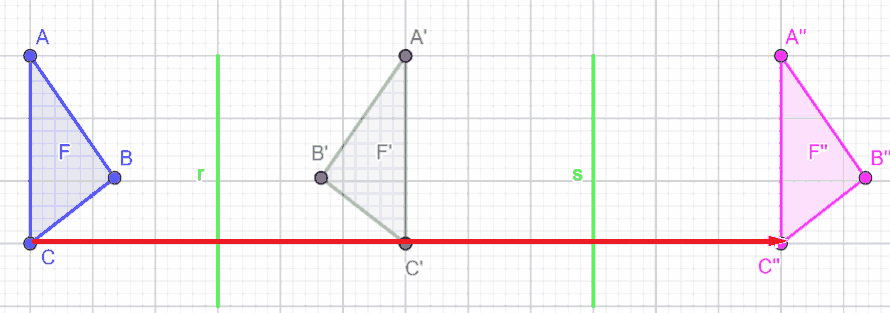
Per quanto concerne il VERSO della traslazione si nota che esso è PERPENDICOLARE rispetto agli ASSI di SIMMETRIA.
Ora soffermiamoci ad osservare l'AMPIEZZA della traslazione.
Indichiamo la DISTANZA tra i due ASSI DI SIMMETRIA
r e s, con il vettore
.
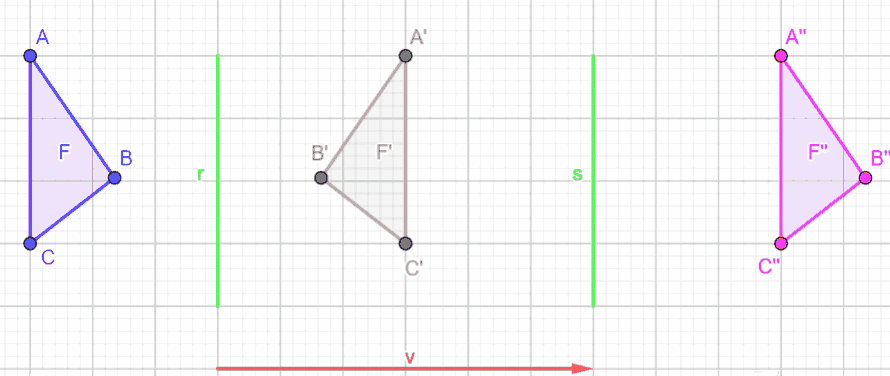
Possiamo verificare facilmente che il vettore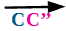
è il doppio del vettore .
Quindi possiamo concludere che, il PRODOTTO di due SIMMETRIE ASSIALI con ASSI PARALLELI è una TRASLAZIONE di vettore PERPENDICOLARE agli assi di simmetria e di modulo DOPPIO della loro distanza.
Nella prossima lezione vedremo alcuni casi particolari di simmetrie assiali.
