TRASFORMAZIONI GEOMETRICHE
Osserviamo l'immagine riportata sotto:

Abbiamo disegnato due bandiere. La bandiera B risulta essere rimpicciolita rispetto alla bandiera A. Tuttavia, ad ogni punto della bandiera A corrisponde un solo punto della bandiera B e viceversa.
Ora osserviamo questa seconda immagine:

In questo caso la bandiera B risulta essere deformata rispetto alla bandiera A, ma anche in questo caso, ad ogni punto della bandiera A corrisponde un solo punto della bandiera B e viceversa.
Infine osserviamo questa terza immagine:
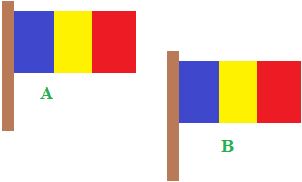
Qui le due bandiere A e B sono identiche nelle dimensioni, e anche in questo caso, ad ogni punto della prima bandiera corrisponde un solo punto della seconda e viceversa, ma le due bandiere risultano essere spostate l'una dall'altra.
In tutti e tre i casi possiamo dire che c'è stata una TRASFORMAZIONE GEOMETRICA cioè, dalla figura A abbiamo ottenuto la figura B i cui PUNTI sono in CORRISPONDENZA BIUNIVOCA con i punti della figura A.
La figura B si dice TRASFORMATA o CORRISPONDENTE della figura A nella trasformazione considerata.
Come si è visto, in seguito alla trasformazione geometrica, si hanno dei cambiamenti nel passaggio dalla figura A alla figura B. Alcune proprietà geometriche possono rimanere invariate: esse prendono il nome di INVARIANTI della trasformazione.
Ad esempio, a restare invariata può essere la forma, o laposizione o le dimensioni.
Le proprietà geometriche che cambiano in seguito alla trasformazione prendono, invece, il nome di VARIANTI della trasformazione.






