PUNTI SIMMETRICI RISPETTO AD UNA RETTA
- Il punto
- La retta
- Rette perpendicolari
- Il segmento
- Gli angoli
- Punti simmetrici rispetto ad una retta
Consideriamo i PUNTI
A e A'
e la RETTA r:
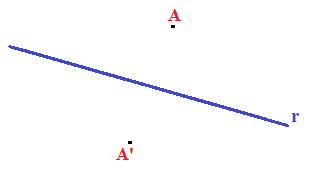
Ora tracciamo il SEGMENTO che unisce i punti A e A':
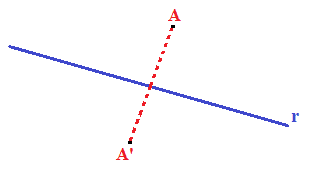
Disegniamo il PUNTO MEDIO del segmento AA' e lo chiamiamo M:
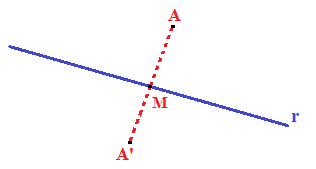
Ora osserviamo che la retta r è PERPENDICOLARE al segmento AA' nel suo punto medio. Infatti essi, incontrandosi, formano 4 angoli uguali, ognuno di 90°.
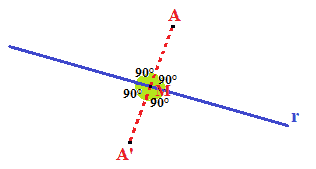
Per questa ragione, i due punti A e A', si dicono SIMMETRICI.
La retta r prende il nome di ASSE DI SIMMETRIA.
Quindi possiamo dire che due PUNTI si dicono SIMMETRICI rispetto ad una retta quando la RETTA è PERPENDICOLARE al SEGMENTO che li UNISCE nel suo PUNTO MEDIO.
Nelle prossime lezioni vedremo come, queste nozioni, possono esserci utili nella ricerca delle coordinate di punti simmetrici.






