SIMMETRIA ASSIALE
Disegniamo, su un piano α (che si legge alfa), la retta r.
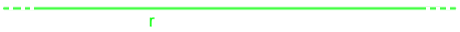
Ora disegniamo un punto P tale che esso non appartenga alla retta r.
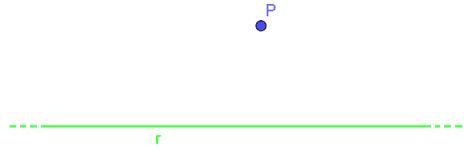
Quindi tracciamo la retta perpendicolare alla retta r e passante per il punto P: chiamiamo tale retta s.
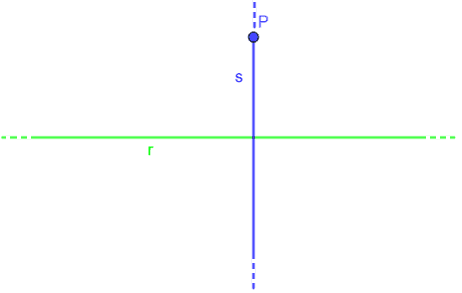
Chiamiamo H il punto di intersezione delle due rette.
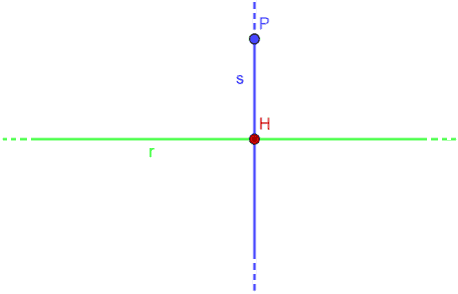
Ora, misuriamo il segmento HP e tracciamo, sempre sulla retta s, dalla parte opposta a P, il segmento HP' tale che abbia la stessa misura di HP.
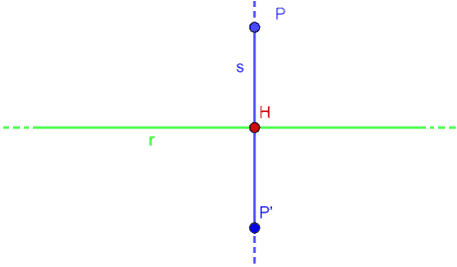
Il punto P' viene detto SIMMETRICO di P rispetto alla retta r.
Questa SIMMETRIA è detta ASSIALE dato che i punti P e P' sono simmetrici rispetto ad un ASSE.
Possiamo considerare la SIMMETRIA ASSIALE come una sorta di ribaltamento del nostro punto P: in altre parole è come se il punto P uscisse dal piano α per ritornarvi dopo aver compituo una rotazione di 180° intorno alla retta r.
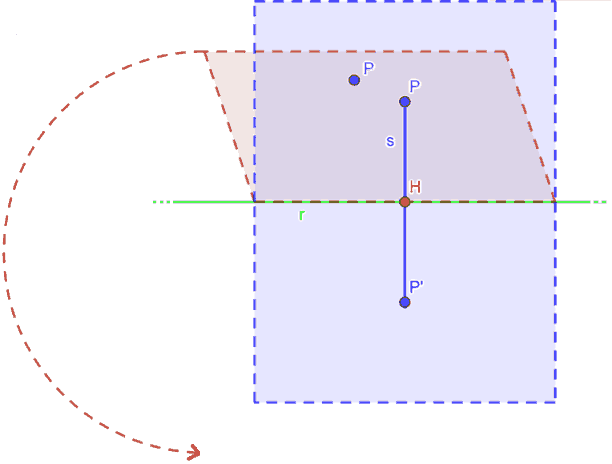
Possiamo quindi dire che la SIMMETRIA ASSIALE è un MOVIMENTO INVERSO individuato da una retta r che prende il nome di ASSE di SIMMETRIA.
Per indicare che la retta r è il nostro ASSE di SIMMETRIA useremo il simbolo
Sr
che si legge
asse si simmetria r.
Nella prossima lezione continueremo a parlare di simmetria assiale e vedremo come possiamo costruire due figure piane simmetriche tra loro.






