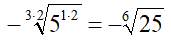PROPRIETA' INVARIANTIVA DEI RADICALI
- Radicali quadratici
- Radicali cubici
- Radicali di indice n
- Radicali con indice dispari
- Prima proprietà fondamentale dei radicali
- Elevamento a potenza
- L'insieme dei numeri naturali
- Simboli usati per l'insieme dei numeri naturali
- Proprietà delle potenze
- L'insieme dei numeri reali
Dato un radicale di indice n, il cui radicando è una potenza am, tale che a sia un numero reale POSITIVO o NULLO, il suo valore non cambia se MOLTIPLICHIAMO:
- l'INDICE n del radicale;
- e l'ESPONENTE m del radicando;
per uno stesso numero naturale p, DIVERSO DA ZERO.
In altre parole possiamo scrivere:
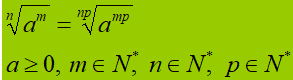
che si legge
la radice di indice n di a elevato ad m
è uguale
alla radice di indice n per p di a elevato ad m per p
con
a maggiore o uguale a zero
m, n e p appartenenti ad enne asterisco (ovvero all'insieme dei numeri naturali escluso lo zero).
Per la validità della proprietà invariantiva dei radicali, abbiamo posto come condizione che
a ≥ 0.
Questo perché, se a è minore di zero, la proprietà invariantiva potrebbe non sempre essere valida.
Iniziamo col dimostrare la PROPRIETA' INVARIANTIVA DEI RADICALI.
Partiamo da una premessa
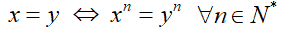
che si legge
x uguale y equivale logicamente a x elevato ad n uguale ad y elevato ad n
per qualunque n appartenente ad enne asterisco (ovvero l'insieme dei numeri naturali escluso lo zero).
Partiamo dalla relazione appena scritta, ovvero:
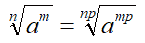
Eleviamo, primo e secondo membro a np:
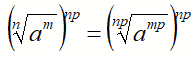
Applicando, a primo membro, la PROPRIETA' di una POTENZA DI POTENZA, possiamo scrivere:
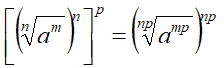
Dato che la PRIMA PROPRIETA' FONDAMENTALE DEI RADICALI ci dice che
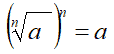
possiamo scrivere:
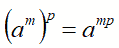
Applicando a primo membro, ancora una volta la proprietà di una potenza di potenza, abbiamo:
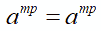
Da cui
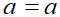
Una volta dimostrata la proprietà invariantiva dei radicali, vediamo come possiamo usarla.
Supponiamo di voler trasformare un radicale quadratico in un radicale di indice sei. Ad esempio:
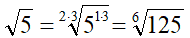
Oppure immaginiamo di voler trasformare un radicale cubico in un radicale di indice ventisette. Ad esempio:
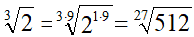
Ora facciamo una precisazione. Abbiamo detto che, affinché la proprietà invariantiva dei radicali valga è necessario che
a ≥ 0.
Quindi, ad esempio, non potremmo trasformare il radicale
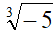
in un radicale di indice 6, dato che -5 è un numero negativo. Sappiamo, però, che essendo un radicale di indice dispari, possiamo scriverlo anche nel modo seguente:
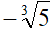
A questo punto, essendo il radicando positivo, possiamo applicare la proprietà invariantiva e trasformare il nostro radicale in un radicale di indice 6: