DISEGNARE IL GRAFICO DI UNA PARABOLA

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Parabola
• Parabola con vertice nell'origine degli assi
• Equazione della parabola con asse di simmetria parallelo all'asse delle y
• Equazione della parabola
• Fuoco e direttrice della parabola
• Intersezione della parabola con gli assi cartesiani
• Intersezione della parabola con gli assi cartesiani
• Discriminante di un'equazione di secondo grado

Vogliamo ora capire quali passi occorre seguire per DISEGNARE correttamente il GRAFICO di una PARABOLA.

Le cose da fare sono:

• stabilire la CONCAVITA' della parabola, verso l'alto o verso il basso;
• determinare le coordinate del VERTICE della parabola;
• stabilire l'equazione dell'ASSE di SIMMETRIA;
• stabilire le coordinate del punto di INTERSEZIONE con l'asse delle y;
• stabilire se vi sono punti di INTERSEZIONE con l'asse delle x e, nel caso, trovarne le coordinate.

In genere, nel disegnare la parabola si procede anche ad individuare:

• il suo FUOCO;
• la sua DIRETTRICE

anche se essi non sono indispensabili per disegnare la parabola.

Esempio:

disegniamo la parabola y = x² + 4x - 5.

Dunque l'equazione della parabola è:

y = x² + 4x - 5.

Ricordiamo che l'equazione generale della parabola è:

y = ax² + bx + c.

Iniziamo con lo stabilire la concavità della parabola. Essa dipende dal valore di a.

Nel nostro caso

a = 1

dunque

a > 0.

Quindi la parabola ha CONCAVITA' rivolta VERSO L'ALTO.

Passiamo a determinare le coordinate del VERTICE. Prima, ci calcoliamo il DISCRIMINANTE che ci servirà anche nel calcolo delle coordinate del fuoco.

Δ = b² - 4ac = 4²- 4 (1) (-5) = 16 + 20 = 36.

Passiamo a calcolare le coordinate del vertice:

V (-b/2a ; -Δ/4a)

V (-4/2 ; -36/4)

V (-2 ; -9).

L'equazione dell'ASSE DI SIMMETRIA è;

x = -b/2a = -4/2 = -2

x = -2.

Ora cerchiamo il PUNTO DI INTERSEZIONE con l'asse delle y risolvendo il sistema:

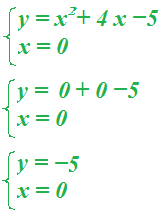
A ( 0; -5).

Ora cerchiamo il PUNTO DI INTERSEZIONE con l'asse dellex risolvendo il sistema:

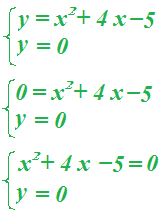
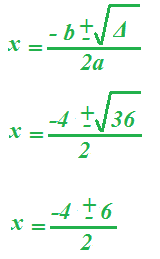
x₁ = (-4 - 6)/ 2 = -5

x₂ = (-4 + 6)/ 2 = 1.

I due punti di intersezione della parabola con l'asse delle x sono:

B (-5; 0)

C (1; 0).

Ora troviamo il FUOCO della parabola:

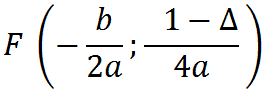
-b/2a = -4/2 = -2

(1- Δ)/ 4a = (1 - 36)/ 4 = -35/4.

F (-2; -35/4).

Per concludere troviamo la DIRETTRICE:

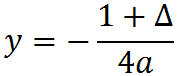
y = - (1 + 36)/ 4 = -37/4.

Ora disegniamo gli assi cartesiani e riportiamo su di essi, VERTICE, ASSE DI SIMMETRIA, PUNTI DI INTERSEZIONE della PARABOLA con gli ASSI CARTESIANI:

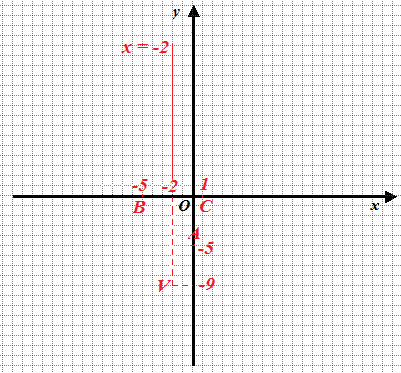
Ora siamo in grado di DISEGNARE il GRAFICO della PARABOLA:

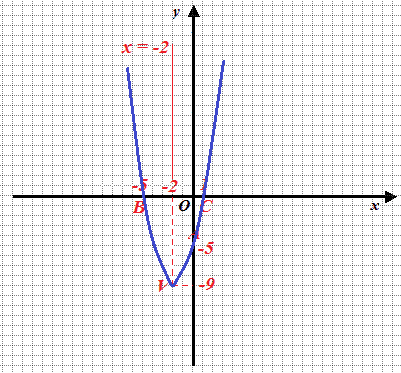
Per completare, riportiamo anche il FUOCO e la DIRETTRICE:

Esercizi su questo argomento:

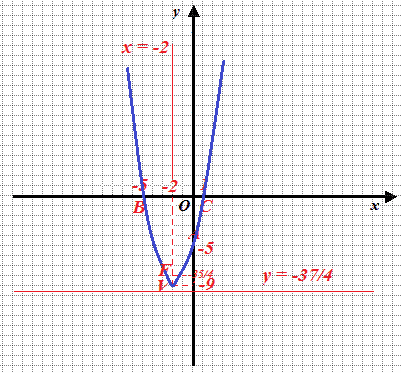
• Esercizio 4 - Fuoco e direttrice della parabola
• Esercizio 5 - Fuoco e direttrice della parabola
• Esercizio 6 - Rappresentazione della parabola sul piano cartesiano
• Esercizio 7 - Fuoco e direttrice della parabola
• Esercizio 8 - Fuoco e direttrice della parabola

Lezione precedente - Lezione successiva

Indice degli argomenti sulla parabola

Pubblicità/Advertising