LA PARABOLA
- Funzioni matematiche
- Le funzioni
- Rappresentazione grafica di una funzione
- Assi cartesiani ortogonali
Supponiamo di voler disegnare il GRAFICO della FUNZIONE
y = x2.
Predisponiamo la nostra consueta tabella:
| x | y |
|---|---|
| -1 | 1 |
| -2 | 4 |
| -3 | 9 |
| -4 | 16 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Ora riportiamo i punti appena individuati sugli ASSI CARTESIANI:
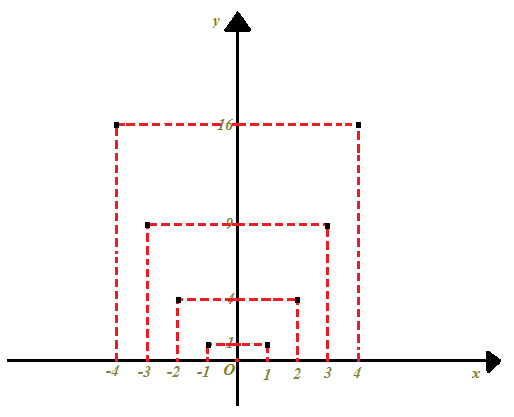
Colleghiamo i punti individuati ed avremo il grafico della funzione:
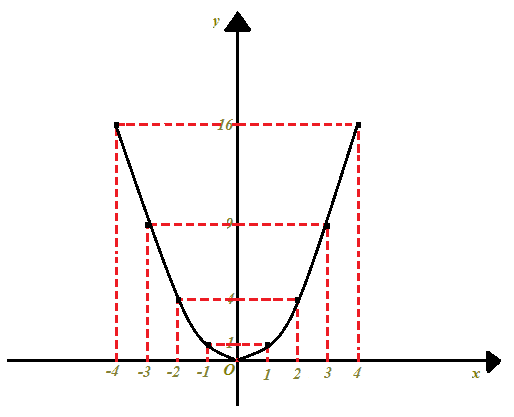
La curva che abbiamo disegnato prende il nome di PARABOLA.
Notiamo che, nella parabola che abbiamo appena disegnato, l'asse delle y rappresenta l'ASSE SI SIMMETRIA, in altre parole essa divide la parabola in due parti specularmente uguali.
Inoltre, osservando l'immagine in alto, vediamo che esiste un solo PUNTO DELLA PARABOLA che APPARTIENE all'ASSE DI SIMMETRIA: tale punto, nel nostro grafico, è l'origine degli assi. Questo punto prende il nome di VERTICE.






