EQUAZIONE DELLA PARABOLA CON ASSE DI SIMMETRIA PARALLELO ALL'ASSE DELLE Y

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Parabola
• Parabola con vertice nell'origine degli assi
• Identità ed equazioni
• Traslazione degli assi cartesiani
• Rette parallele
• Retta parallela all'asse delle y

Nelle lezioni precedenti abbiamo visto che l'equazione della PARABOLA che ha come VERTICE l'ORIGINE DEGLI ASSI e come ASSE DI SIMMETRIA l'ASSE DELLE y è la seguente

y = ax²

con

a ≠ 0.

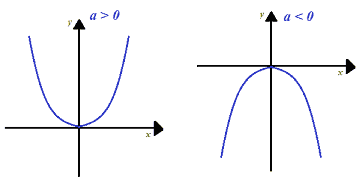
Inoltre si è visto che la parabola ha la concavità rivolta verso l'alto o verso il basso a seconda che

a > 0

oppure

a < 0.

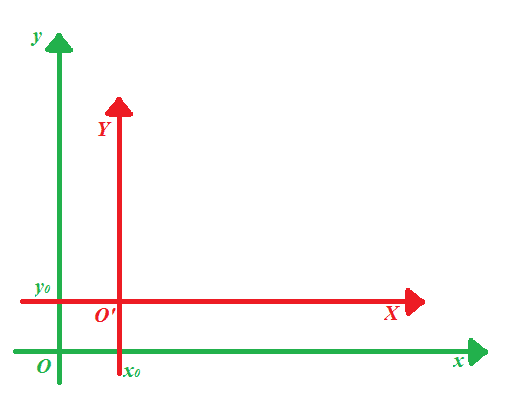
Ora vogliamo effettuare una TRASLAZIONE DEGLI ASSI CARTESIANI portando l'origine degli assi nel punto O' di coordinate (x₀; y₀)

Ora disegniamo la parabola avente come vertice O':

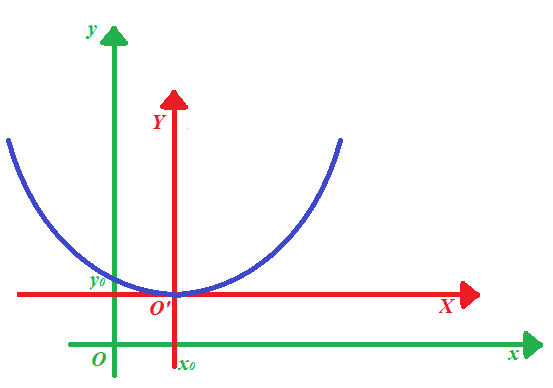
La parabola appena disegnata ha come equazione

Y = aX².

Ma noi sappiamo che la relazione che lega i due sistemi di assi cartesiani è la seguente:

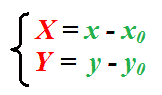
Quindi, sostituiamo, nell'equazione della parabola e abbiamo:

y - y₀ = a (x - x₀)².

In questo modo abbiamo scritto l'equazione della nostra parabola facendo riferimento agli assi cartesiani x e y (e non più agli assi X e Y).

Risolviamo ed otteniamo:

y - y₀ = a (x² + x₀² - 2xx₀ )

y - y₀ = ax² + ax₀² - 2axx₀

y = ax² + ax₀² - 2axx₀ + y₀.

Ora poniamo

- 2ax₀ = b

e poniamo

ax₀² + y₀= c.

Avremo:

y = ax² + ax₀² - 2axx₀ +y₀

y = ax² + bx + c.

Quindi possiamo dire che l'equazione:

y = ax² + bx + c

è l'equazione di una PARABOLA avente l'ASSE SI SIMMETRIA PARALLELO all'ASSE delle y e avente il vertice nel punto di coordinate (x₀ ; y₀).

Ora determiniamo le coordinate del vertice della parabola facendo riferimento agli assi cartesiani x e y.

Abbiamo detto che la relazione che lega i due sistemi di assi cartesiani è la seguente:

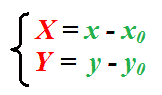
Ma poiché la nostra parabola ha il vertice nell'origine degli assi X e Y, possiamo scrivere:

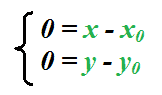
da cui otteniamo:

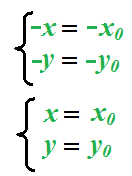
Le coordinate del vertice le troviamo ricordando che abbiamo posto:

- 2ax₀ = b

e

ax₀² +y₀= c.

Innanzitutto poniamo a sistema:

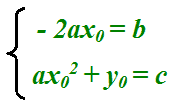
Ora, poiché

x = x₀

y = y₀

effettuiamo le opportune sostituzioni:

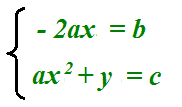
Risolviamo la prima equazione:

-2ax = b

2ax = -b

x = -b/2a.

Sostituiamo, nella seconda equazione, il valore della x e cerchiamo il valore della y:

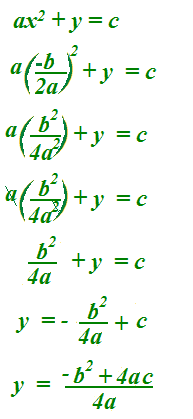
Poiché noi sappiamo che:

Δ = b² - 4ac.

Avremo che:

-Δ = -b² + 4ac.

E quindi:

y = -Δ/ 4a.

Quindi, le coordinate del vertice della nostra parabola sono:

V ( -b/2a ; -Δ/ 4a).

Notiamo ancora che, l'asse di simmetria, è la retta parallela all'asse delle y passante per il punto di coordinate (x₀; 0). Quindi l'ASSE DI SIMMETRIA è la retta di equazione:

x = -b/2a.

Nella lezione che segue vedremo un altro modo per giungere all'equazione della parabola.

Lezione precedente - Lezione successiva

Indice degli argomenti sulla parabola

Pubblicità/Advertising