AREA DEL SEGMENTO CIRCOLARE
- La circonferenza e il cerchio
- Corde di una circonferenza
- Segmento circolare
- Area del settore circolare
- Area del triangolo
- Triangolo isoscele
- Somma degli angoli interni di un triangolo
- Triangolo equilatero
- Poligoni equiangoli poligoni equilateri poligoni regolari
- Area di un poligono regolare conoscendo il lato
- Area del triangolo conoscendo i lati
Si chiama SEGMENTO CIRCOLARE ognuna delle due PARTI di CERCHIO limitata da una CORDA e dai DUE ARCHI corrispondenti:
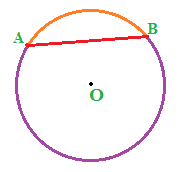
Ora ci poniamo il problema di determinare l'AREA del SEGMENTO CIRCOLARE ALB che nell'immagine sottostante abbiamo evidenziato in giallo chiaro:
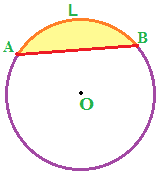
Osserviamo l'immagine che segue:
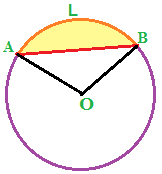
Essa ci permette di comprendere che, possiamo ottenere l'area del SEGMENTO CIRCOLARE ALB SOTTRAENDO, dall'area del SETTORE CIRCOLARE ALBO l'area del TRIANGOLO AOB. Osserviamo, inoltre, che il triangolo AOB è un triangolo isoscele in quanto ha due lati congruenti che sono i raggi del cerchio.
Ipotizziamo, ora, di voler conoscere l'AREA del SEGMENTO CIRCOLARE AMB che nell'immagine sottostante abbiamo evidenziato in rosa:
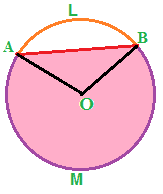
E' evidente che possiamo ottenere l'area del SEGMENTO CIRCOLARE AMB AGGIUNGENDO, all'area del SETTORE CIRCOLARE AMBO l'area del TRIANGOLO isoscele AOB.
Quindi possiamo generalizzare dicendo che:
- se il SEGMENTO CIRCOLARE è MINORE della SEMICIRCONFERENZA, la sua AREA si ottiene come DIFFERENZA tra l'AREA del SETTORE CIRCOLARE che insiste sullo stesso arco e l'AREA del TRIANGOLO ABO;
- se il SEGMENTO CIRCOLARE è MAGGIORE della SEMICIRCONFERENZA, la sua AREA si ottiene come SOMMA tra l'AREA del SETTORE CIRCOLARE corrispondente e l'AREA del TRIANGOLO ABO.
Esempio 1:
calcolare l'area del segmento circolare che appartiene ad un cerchio che ha il raggio di cm 18 ed il cui angolo al centro misura 60°.
Iniziamo col calcolarci l'area del settore circolare. Chiamiamo tale area ASTC
ASTC = (π x r2 x n)/ 360 =
= (3,14 x 182 x 60)/ 360 =
= 61.041,6/ 360 = 169,56 cm2.
Ora troviamo l'area del triangolo che chiamiamo AT. Noi conosciamo la misura di due suoi lati, trattandosi di un triangolo isoscele, ma non abbiamo la misura dell'altezza.
Però sappiamo che l'angolo al centro misura 60°: esso è anche un angolo del nostro triangolo. Questo significa che il nostro triangolo è un triangolo equiangolo e di conseguenza esso è anche equilatero. Cerchiamo di capire perché giungiamo a questa conclusione. La somma degli angoli interni di un triangolo è sempre pari a 180°. Se l'angolo al vertice misura 60°, la somma degli angoli alla base misura 120° (180° - 60°). Poiché gli angoli alla base di un triangolo isoscele sono congruenti, ognuno di essi è ampio 60° (120° : 2). Il triangolo, quindi, è equiangolo e equilatero.
Il triangolo equilatero è un poligono regolare e, dunque, come ogni poligono regolare possiamo trovare la sua area conoscendo solamente la misura del lato. Si tratterà di applicare la formula seguente:
AT =l2 x φ
dove
AT = area del triangolo
l = lato
φ (che si legge fi) = una costante
che varia a seconda dei lati del poligono e che nel triangolo equilatero è pari a 0,433.
AT = 182 x 0,433 = 140,292 cm2.
Conoscendo la misura dei tre lati del triangolo avremmo potuto calcolare l'area anche applicando la formula di Erone.
Ora possiamo calcolare l'area del segmento circolare, che indichiamo con ASGC . Poiché esso è minore della semicirconferenza avremo:
ASGC = ASTC - AT = 169,56 - 140,292 = 29,268 .
L'area del segmento circolare misura 29,268 cm2.
Esempio 2:
calcolare l'area del segmento circolare corrispondente ad un angolo al centro ampio 300° e appartenente ad un cerchio il cui raggio misura 12 cm.
Iniziamo col calcolarci l'area del settore circolare:
ASTC = (π x r2 x n)/ 360 =
= (3,14 x 122 x 300)/ 360 =
= 135.648/ 360 = 376,8 cm2.
Ora troviamo l'area del triangolo. Noi conosciamo la misura di due suoi lati, trattandosi di un triangolo isoscele, ma non abbiamo la misura dell'altezza.
Però sappiamo che l'angolo al centro misura 300°. Quindi, l'angolo al vertice del triangolo sarà pari a 60° (360 - 300). Di conseguenza, il nostro triangolo è un triangolo equiangolo ed equilatero. Perciò applichiamo la formula che ci permette di trovare l'area di un poligono regolare conoscendo il suo lato:
AT = l2 x φ =
= 122 x 0,433 = 62,352 cm2.
Ora possiamo calcolare l'area del segmento circolare. Poiché esso è maggiore della semicirconferenza avremo:
ASGC = ASTC + AT = 376,8 + 62,352 = 439,152 cm2.
L'area del segmento circolare misura 439,152 cm2.






