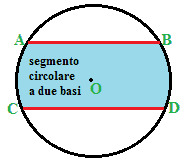
SEGMENTO CIRCOLARE
- La circonferenza e il cerchio
- Parti di una circonferenza e di un cerchio
- Corde di una circonferenza
- Archi di una circonferenza
- Il punto
- Rette parallele
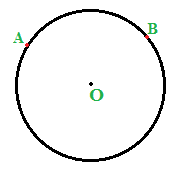
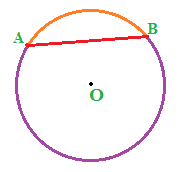
Dato un CERCHIO, il cui centro è O, consideriamo DUE PUNTI A e B appartenenti alla circonferenza:
Ora tracciamo la CORDA AB:
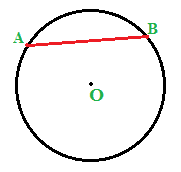
La corda disegnata individua DUE ARCHI
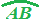 .
.
Nell'immagine sottostante li abbiamo evidenziati uno con il colore arancio e l'altro con il colore viola.
Ognuna delle due PARTI di CERCHIO limitata dalla CORDA e dai DUE ARCHI corrispondenti prende il nome di SEGMENTO CIRCOLARE AD UNA BASE:
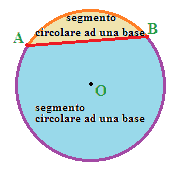
In altre parole possiamo dire che UNA CORDA DIVIDE il CERCHIO in due parti: ognuna di esse si chiama SEGMENTO CIRCOLARE AD UNA BASE.
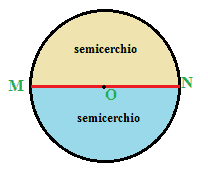
Se la CORDA che disegniamo è il DIAMETRO, il cerchio risulta diviso in DUE PARTI UGUALI ognuna delle quali si chiama SEMICERCHIO:
Se in un CERCHIO disegniamo DUE CORDE PARALLELE, la PARTE DI CERCHIO COMPRESA TRA LE DUE CORDE prende il nome di SEGMENTO CIRCOLARE A DUE BASI: