AREA DEL SETTORE CIRCOLARE: PROBLEMI
- Area del settore circolare
- Area del settore circolare: formule inverse
- Settore circolare
- Lunghezza di un arco
Nelle lezioni precedenti abbiamo visto come si calcola l'AREA DI UN SETTORE CIRCOLARE e le relative FORMULE INVERSE.
In questa lezione vedremo come applicare le nozioni apprese a dei problemi.
Problema 1:
calcolare l'area di un settore circolare ampio 45° appartenente ad un cerchio il cui raggio misura 18 cm.
In questo caso noi conosciamo l'ampiezza del settore circolare e il raggio del cerchio, quindi è sufficiente applicare la formula relativa all'area del settore circolare ovvero:
A = (π x r2 x n)/ 360 =
= (3,14 x 182 x 60)/ 360 =
= (3,14 x 324 x 60)/ 360 =
= 61.041,6/ 360 = 169,56 cm2.
Problema 2:
calcolare il raggio di un settore circolare che ha l'area di cm2 141,30 e la cui ampiezza è pari a 72°.
In questo caso noi conosciamo l'area e l'ampiezza del settore circolare e vogliamo trovare il raggio. Dobbiamo, quindi, applicare la formula inversa:
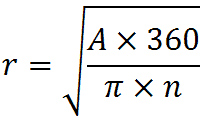
Sostituendo i dati del problema, avremo:
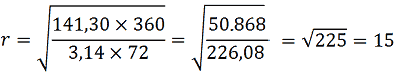
Il raggio del nostro cerchio misura 15 cm.
Problema 3:
calcolare l'ampiezza di un settore circolare che ha l'area di m2 1,05 ed appartiene ad un cerchio il cui raggio misura 2 m.
In questo caso noi conosciamo l'area del settore circolare ed il raggio del cerchio. Dobbiamo, quindi, applicare la formula inversa:
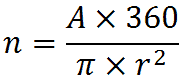
Sostituendo i dati del problema, avremo:
n = (1,05 x 360)/ (3,14 x 22) =
= 378/ 12,56 = 30°.
L'ampiezza del settore circolare è di 30°.
Problema 4:
calcolare la lunghezza dell'arco che limita un settore circolare sapendo che l'area di tale settore è di 39 cm2 e che esso appartiene ad un cerchio il cui raggio misura cm 6.
In questo caso noi conosciamo l'area del settore circolare ed il raggio del cerchio e dobbiamo calcolare la lunghezza dell'arco che limita tale settore circolare. Possiamo applicare la formula che, partendo dai valori di A ed r, ci permette di determinare direttamente il valore di l. Ovvero
l = 2A/ r = (2 x 39)/ 6 = 78/ 6 = 13 cm.
La lunghezza dell'arco è di 13 cm.






