AREA DI UN POLIGONO REGOLARE CONOSCENDO UN LATO
- Area dei poligoni
- Area di un poligono regolare
- Area di un poligono regolare e formule inverse
- Apotema di un poligono regolare
- Poligoni equiangoli poligoni equilateri poligoni regolari
- Misure di superficie
- Apotema di un poligono
- Perimetro di un poligono
Nella lezione precedente abbiamo visto che, in un POLIGONO REGOLARE, il RAPPORTO tra l'APOTEMA del poligono e il LATO è sempre COSTANTE. Abbiamo indicato tale valore con f e abbiamo detto che
f = a/l
dove
f = costante del poligono
a = apotema
l = lato.
Ora supponiamo di avere un esagono e di conoscere solamente la misura del suo lato.
La formula per trovare l'area dell'esagono è:
A = (P x a)/ 2.
Trattandosi di un esagono il perimetro è dato da:
P = 6 x l.
Se sostituiamo tale formula in quella dell'area avremo:
A = (6 x l x a)/ 2.
Sappiamo però che l'apotema è uguale a
a = l x f
e che, nel caso dell'esagono, f è uguale a 0,866. Quindi possiamo scrivere che l'apotema è uguale a:
a = l x 0,866.
Ora, riprendiamo la formula dell'area e sostituiamo in essa il valore dell'apotema. Ovvero:
A = (6 x l x a)/ 2
A = (6 x l x l x 0,866)/ 2.
Moltiplicando l x l possiamo scrivere:
A = (6 x l2 x 0,866)/ 2.
Mentre, semplificando il 6 con il 2 otterremo:
A = (3 x l2 x 0,866)/ 1 = 3 x l2 x 0,866.
Infine, moltiplicando il 3 per la costante 0,866 avremo:
A = 3 x l2 x 0,866 = l2 x 2,598.
Quindi:
A = l2 x 2,598.
Ovviamente, da questa formula ricaviamo che:
A/ l2 = 2,598.
Il discorso appena fatto per l'esagono vale per qualsiasi altro poligono regolare.
Quindi possiamo dire che in qualsiasi POLIGONO REGOLARE il RAPPORTO tra l'AREA e il QUADRATO del LATO è uguale ad una COSTANTE. Il valore di tale costante dipende dal NUMERO dei LATI del poligono.
E possiamo anche dire che l'AREA di un POLIGONO REGOLARE è dato dal PRODOTTO tra il QUADRATO della misura del LATO e la COSTANTE del poligono considerato. Chiamiamo tale costante
φ
che si legge
fi.
Quindi possiamo scrivere che
A = l2 x φ
e di conseguenza
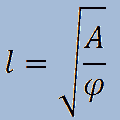
Riportiamo, nella tabella che segue, il valore della costante φ per i diversi poligoni regolari:
| POLIGONO | COSTANTE |
|---|---|
| Triangolo equilatero | 0,433 |
| Quadrato | 1 |
| Pentagono regolare | 1,720 |
| Esagono regolare | 2,598 |
| Ettagono regolare | 3,634 |
| Ottagono regolare | 4,828 |
| Ennagono regolare | 6,182 |
| Decagono regolare | 7,694 |
Esempio 1:
calcolare l'area di un ottagono regolare il cui lato misura 20 cm.
Applichiamo la formula vista:
A = l2 x φ.
Trattandosi di un ottagono regolare il valore di φ è uguale a 4,828. Quindi avremo:
A = l2 x φ = 202 x 4,828 = 400 x4,828 = cm2 1.931,2.
Esempio 2:
calcolare il perimetro di un pentagono regolare la cui area misura cm2 50.
Applichiamo la formula inversa appena vista in modo da trovare la misura del lato:
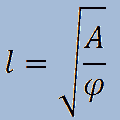
Trattandosi di un pentagono regolare il valore di φ è uguale a 1,720. Quindi avremo:
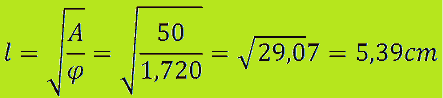
Per conoscere il perimetro è sufficiente moltiplicare il lato per 5 dato che il pentagono ha 5 lati:
P = 5 x 5,39 cm = 26,95 cm.






