DOMINIO DI UNA FUNZIONE ALGEBRICA IRRAZIONALE FRATTA
- Funzioni reali di variabile reale
- Classificazione delle funzioni reali
- Dominio di una funzione algebrica irrazionale intera
- Dominio di una funzione algebrica razionale fratta
- L'insieme dei numeri reali
- Disequazioni fratte
- Differenza di due insiemi
- Intervalli
- Unione di due insiemi
- Le frazioni
- Radice quadrata
- Estrazione di radice da un intero
Una FUNZIONE IRRAZIONALE FRATTA è una funzione nella quale:
- la variabile indipendente x si trova sotto il segno di radice. Per questa ragione essa è detta IRRAZIONALE;
- la variabile indipendente x si trova al denominatore di una frazione. Per questa ragione essa è detta FRATTA.
In altre parole una FUNZIONE IRRAZIONALE FRATTA è una funzione del tipo
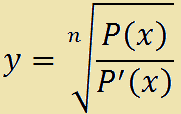
che si legge
y è uguale alla radice ennesima di P con x fratto P primo con x.
Anche in questo caso, come nel caso delle funzioni irrazionali intere, il CAMPO DI ESISTENZA dipende dal valore assunto dall'INDICE DELLA RADICE. Ma, in questo caso, a differenza di quanto accade per le funzioni irrazionali intere, occorre anche porre come condizione che il DENOMINATORE della frazione NON SIA NULLO dato che una frazione che ha al denominatore lo zero è priva di significato.
Quindi, se n è DISPARI, dato che possiamo sempre estrarre la radice di x il campo di esistenza è dato da tutti i valori di x appartenenti all'insieme dei numeri reali eccetto quelli che annullano il denominatore.
Scriveremo allora:
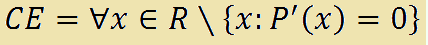
che si legge
campo di esistenza uguale a qualunque x appartenente ad R meno l'insieme delle x tali che P primo con x è uguale a zero.
Se n è PARI possiamo estrarre la radice di P(x)/P'(x) solamente se il radicando è positivo o uguale a zero e se, al tempo stesso, il denominatore P'(x) è diverso da zero.
Scriveremo allora:
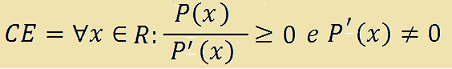
che si legge
campo di esistenza uguale a qualunque x appartenente ad R tale che P con x fratto P primo con x è maggiore o uguale a zero e P primo con x è diverso da zero.
Esempio 1:
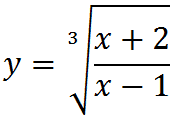
La funzione è irrazionale fratta dato che la x compare sotto il segno di radice e al denominatore della frazione.
Andiamo, allora, ad osservare l'indice della radice. Esso è dispari, infatti
n = 3.
Quindi il campo di esistenza è dato dall'insieme di tutti i numeri reali eccetto quelli che annullano il denominatore. Poniamo allora:
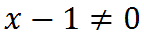
risolviamo e abbiamo
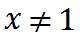
Quindi possiamo dire che:
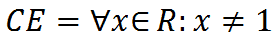
che si legge
campo di esistenza uguale a qualunque x appartenente ad R tale che x è diverso da uno.
Esempio 2:
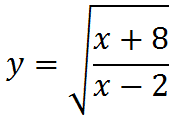
La funzione è irrazionale fratta dato che la x compare sotto il segno di radice e al denominatore della frazione.
Per trovare il campo di esistenza dobbiamo esaminare l'indice della radice. Esso è pari, infatti
n = 2.
Quindi dobbiamo porre come prima condizione che la frazione sia maggiore o uguale a zero. Ovvero
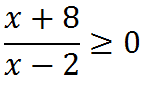
Dallo studio delle disequazioni sappiamo che per risolvere questa disequazione dobbiamo impostare il sistema:
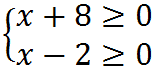
da cui otteniamo:
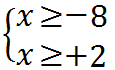
Cerchiamo ora le soluzioni che rendono positiva o nulla la frazione. Esse sono date da:
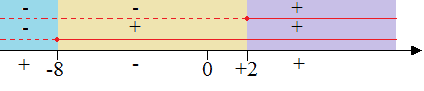
Quindi la nostra frazione è positiva quando:
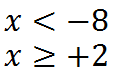
Però, dato che la funzione è fratta, per trovare il suo campo di esistenza dobbiamo escludere i valori di x che annullano il denominatore. Quindi dovrà essere:
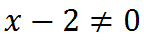
Ovvero:
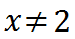
Quindi possiamo scrivere
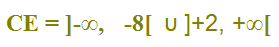
che si legge
campo di esistenza uguale all'intervallo aperto che va da meno infinito a meno otto oppure all'intervallo aperto che va da più due a più infinito.
Ricordiamo che questo
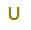
è il simbolo di unione di due insiemi.






