DOMINIO DI UNA FUNZIONE ESPONENZIALE
- Funzioni reali di variabile reale
- Classificazione delle funzioni reali
- Funzione esponenziale
- Elevamento a potenza
- L'insieme dei numeri reali
- Intervalli
- I polinomi
Una FUNZIONE si dice ESPONENZIALE quando la variabile x compare come esponente di una potenza.
La forma tipica di una FUNZIONE ESPONENZIALE è la seguente:
y = ax
che si legge
y è uguale ad a elevato ad x.
In questo caso la BASE della potenza è una COSTANTE (nel nostro esempio la a) e l'esponente è la variabile x. Per questa ragione la funzione viene detta FUNZIONE ESPONENZIALE A BASE COSTANTE.
La nostra costante a deve essere positiva. Ovvero:
a > 0.
Infatti, con la base negativa non avremmo sempre risultati reali.
Se, a dovesse essere uguale ad 1 la funzione sarebbe una costante, cioè y = 1 poiché 1 elevato a qualsiasi valore dà come risultato sempre 1. Quindi il grafico della funzione sarebbe una retta.
In una funzione di questo tipo il CAMPO DI ESISTENZA è dato da qualsiasi x appartenente ai reali.
Quindi possiamo scrivere:
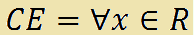
che si legge
campo di esistenza uguale a qualunque x appartenente ai reali.
Esempio:
y = 7x.
La funzione è esponenziale dato che la x compare come esponente di una potenza.
Quindi il campo di esistenza è dato dall'insieme di tutti i numeri reali. Possiamo scrivere:
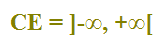
che si legge
campo di esistenza uguale all'intervallo aperto da meno infinito a più infinito.
Tuttavia la FUNZIONE ESPONENZIALE si può presentare anche nella forma seguente:
y = aP(x)
che si legge
y è uguale ad a elevato a P con x.
Anche in questo caso la BASE della potenza è una COSTANTE (nel nostro esempio la a) e di conseguenza si parla sempre di FUNZIONE ESPONENZIALE A BASE COSTANTE.
Anche in questo caso la base a deve essere maggiore di zero.
Tuttavia in questo caso il CAMPO DI ESISTENZA della funzione sarà uguale al CAMPO DI ESISTENZA di P(x).
Esempio 1:
y = 74x+3.
La funzione è esponenziale dato che la x compare come esponente di una potenza.
Il campo di esistenza della funzione è uguale al campo di esistenza di
4x + 3.
Il campo di esistenza di 4x + 3 è dato da tutti i numeri reali. Di conseguenza il campo di esistenza della nostra funzione è dato dall'insieme dei numeri reali.
Esempio 2:
y = 7(4x+3)/x.
La funzione è esponenziale dato che la x compare come esponente di una potenza.
Il campo di esistenza della funzione è uguale al campo di esistenza dell'esponente, ovvero di
4x + 3/x.
Il campo di esistenza di (4x + 3)/x è dato da tutti i numeri reali diversi da zero, dato che nel caso in cui x è uguale a zero il denominatore si annulla.
Di conseguenza il campo di esistenza della nostra funzione è dato dall'insieme dei numeri reali escluso lo zero. Ovvero:
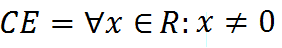
che si legge
campo di esistenza uguale a qualunque x appartenente ai reali tale che x è diverso da zero.
Infine la FUNZIONE ESPONENZIALE si può presentare anche nella forma seguente:
y = [P(x)]P'(x)
che si legge
y è uguale a P con x elevato a P' con x.
In questo caso, a differenza dei precedenti, la BASE della potenza NON E' una COSTANTE: nel nostro esempio essa è P(x). Per questa ragione la funzione viene detta FUNZIONE ESPONENZIALE A BASE VARIABILE.
In questo caso il CAMPO DI ESISTENZA della funzione è dato dai valori di x che rendono positivo P(x) in quanto abbiamo detto che, nel caso in cui la base fosse negativa, potremmo anche non avere risultati reali. Ovvero il CAMPO DI ESISTENZA sarà uguale a:
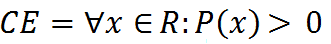
che si legge
campo di esistenza uguale a qualunque x appartenente ad R tale che P con x è maggiore di zero.
Inoltre, come nel caso precedente, dobbiamo tenere conto anche dell'eventuale campo di esistenza di P'(x).
Esempio 3:
y = (x+2)x+3.
La funzione è esponenziale dato che la x compare come esponente di una potenza. Il campo di esistenza della funzione è dato dai valori di x che rendono maggiore di zero la base. Cioè:
x+2 > 0
x > -2.
Poiché l'esponente (x+3) ha come campo di esistenza tutti i numeri reali, la nostra funzione ha come campo di esistenza i valori maggiori di -2. Cioè:
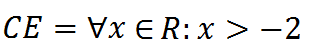
che si legge
campo di esistenza uguale a qualunque x appartenente ad R tale che x è maggiore di meno 2.






