GRAFICO DELLA FUNZIONE COSECANTE
Nelle lezioni precedenti abbiamo visto cosa si intende per COSECANTE e come variano i valori della cosecante al variare dell'angolo α.
In questa lezione, invece, andremo a vedere come possiamo costruire il GRAFICO della FUNZIONE COSECANTE.
Iniziamo col disegnare gli assi cartesiani e riportiamo:
- sull'asse delle ASCISSE i valori degli ANGOLI;
- sull'asse delle ORDINATE il corrispondente valore della COSECANTE.
Come al solito affianchiamo agli assi cartesiani la circonferenza goniometrica in modo da facilitare la costruzione del grafico della funzione.
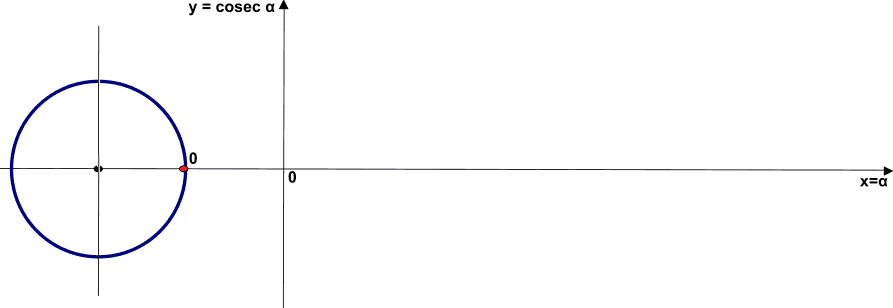
Partiamo dall'angolo di ampiezza 0. Indichiamo l'angolo sugli assi cartesiani nel punto dell'origine. Quando l'angolo vale 0 la sua cosecante, come abbiamo visto nella lezione precedente, non è definita.
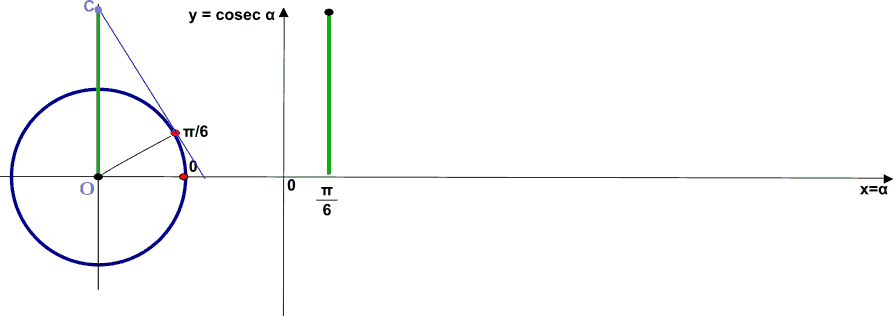
Passiamo a considerare l'angolo π/6. Indichiamo l'angolo sugli assi cartesiani. Disegniamo la cosecante e riportiamo il segmento OC sull'asse delle ordinate. Abbiamo trovato il primo punto della funzione cosecante.
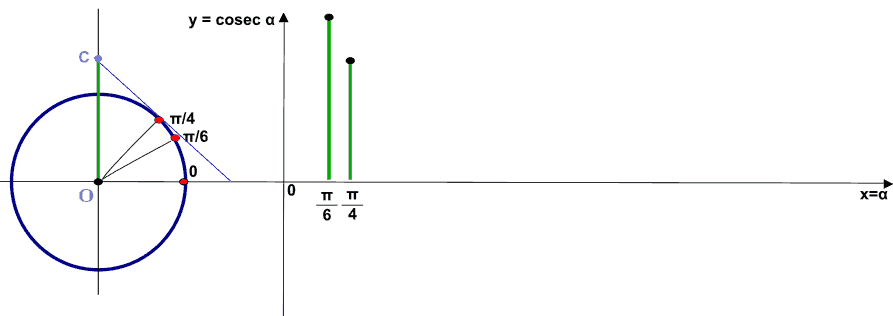
Ora andiamo a considerare l'angolo π/4. Indichiamo l'angolo sugli assi cartesiani. Disegniamo la cosecante e riportiamo il segmento OC sull'asse delle ordinate. Abbiamo trovato il secondo punto della funzione cosecante.
Proseguiamo con altri angoli nella costruzione del grafico della funzione cosecante, che si presenterà nel modo seguente:
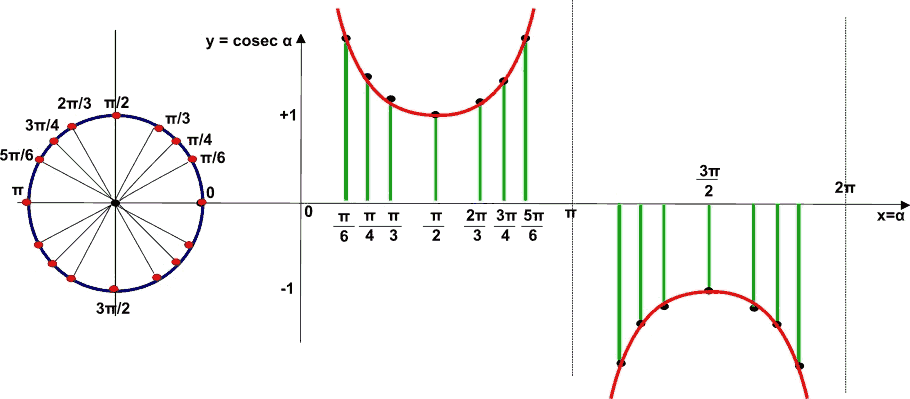
Vediamo allora quali caratteristiche ha la funzione cosecante.
La prima osservazione che possiamo fare è che la funzione NON ASSUME mai i valori COMPRESI tra -1 e +1 ESCLUSI, cioè la funzione può assumere i valori -1 e +1, ma non quelli compresi tra essi.
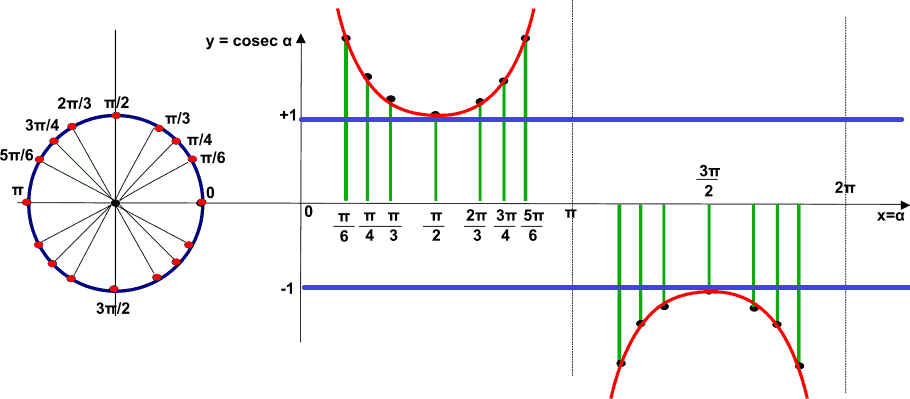
All'origine degli assi la funzione cosecante NON, è DEFINITA, mentre quando l'angolo α ha un'ampiezza di π/2 la funzione assume valore +1.
Vediamo ora cosa accade intorno al punto π:
- per valori inferiori a π, mano a mano che l'angolo si avvicina sempre più a questo valore, la cosecante tende a diventare sempre più grande.
Per questo diciamo che essa tende a
+∞ (che si legge più infinito);
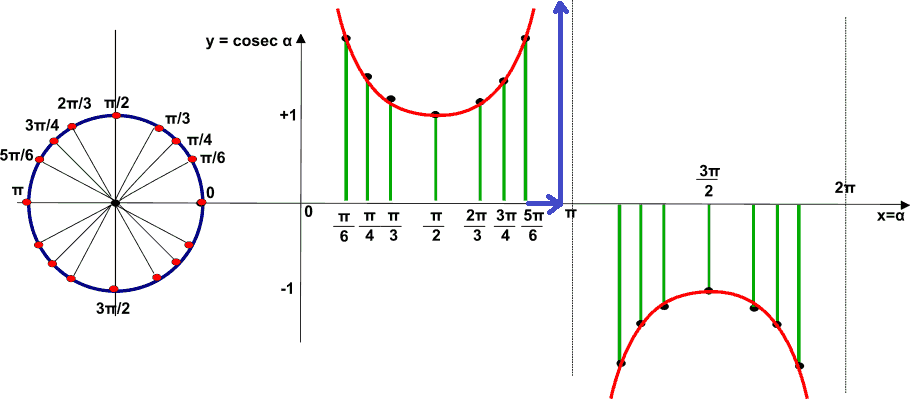
- per valori superiori a π, mano a mano che l'angolo si avvicina sempre più a questo valore la cosecante tende a diventare
sempre più piccola. Per questo diciamo che essa tende a
-∞ (che si legge meno infinito).

Quando il valore dell'angolo α si avvicina a π la cosecante si avvicina sempre più alla retta parallela all'asse delle y di equazione
x = π
che prende il nome di ASINTOTO VERTICALE del grafico.
La stessa cosa si verifica quando l'angolo α si avvicina a 0 e a 2π
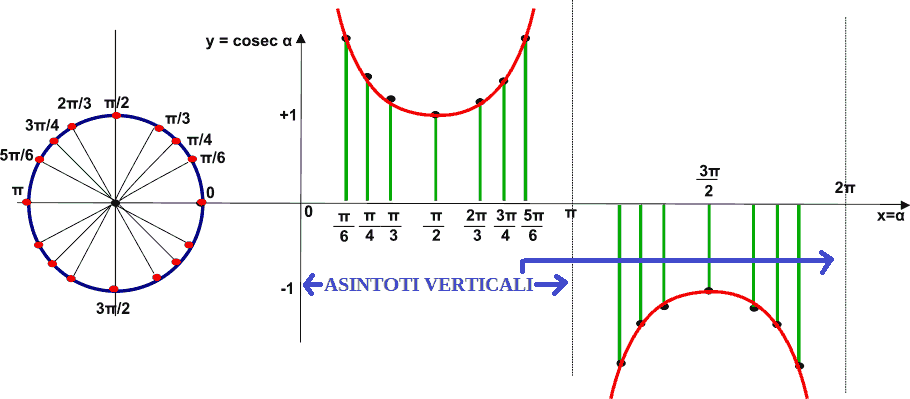
Quindi possiamo dire che gli asintoti verticali sono le rette di equazione
x = 0 + kπ
con k appartenente all'insieme Z, cioè all'insieme dei numeri interi relativi.
Il CODOMINIO della cosecante è dato dall'insieme dei numeri reali, esclusi i valori compresi tra -1 e +1. Il che si scrive nel modo seguente:
R - ]-1 , +1[
che si legge
insieme dei numeri reali R meno l'intervallo aperto -1 + 1
L'intervallo è aperto perché, come abbiamo avuto modo di dire, la funzione cosecante può assumere i valori -1 e +1.
Nella prossima lezione avremo modo di tornare nuovamente sul grafico della funzione cosecante.






