TEOREMA DI PITAGORA E POLIGONO REGOLARE
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Le formule inverse del teorema di Pitagora
- Poligoni equiangoli poligoni equilateri poligoni regolari
- Apotema di un poligono
- Poligoni circoscritti
- La circonferenza e il cerchio
- Triangolo rettangolo
- Apotema di un poligono regolare
Disegniamo un POLIGONO REGOLARE:
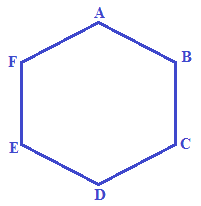
Ricordiamo che un POLIGONO si dice REGOLARE se esso è EQUILATERO ed EQUIANGOLO.
Ora disegniamo l'APOTEMA del nostro poligono, cioè il SEGMENTO che parte dal CENTRO del POLIGONO e cade PERPENDICOLARMENTE su uno dei suoi LATI.
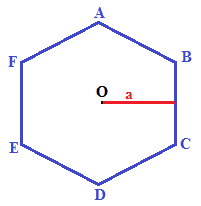
Nella figura sopra abbiamo indicato il centro del poligono con la lettera O e l'apotema con la lettera a.
Ora disegniamo la CIRCONFERENZA CIRCOSCRITTA al poligono e il suo RAGGIO che indichiamo con r:
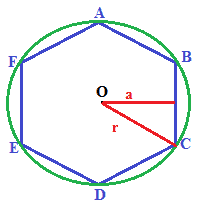
Quello che abbiamo evidenziato nella figura sottostante in viola è un TRIANGOLO RETTANGOLO che ha:
- per ipotenusa il raggio della circonferenza;
- uno dei cateti rappresentato dall'apotema del poligono;
- l'altro cateto uguale alla metà del lato del poligono.
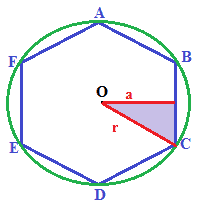
Le formule del TEOREMA DI PITAGORA, in questo caso diventano:
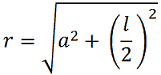
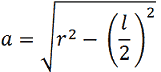
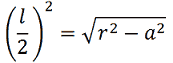
Esempio:
un esagono regolare ha il lato di cm 10. Calcolare la misura del raggio della circonferenza circoscritta.
Per poter calcolare il raggio della circonferenza dobbiamo avere la misura del lato e quella dell'apotema dell'esagono.
Il lato ci è noto: esso misura 10 cm.
Invece non conosciamo la misura dell'apotema, ma dallo studio dei poligoni regolari sappiamo che, per ogni tipo di poligono, il rapporto tra apotema e lato del poligono è una costante. Nel caso dell'esagono si ha:
a/l = 0,8666.
Quindi, se conosciamo il lato dell'esagono, possiamo trovare il suo apotema: basterà moltiplicare il lato per 0,8666. Nel nostro caso avremo:
a = l x0,8666 = 10 x 0,8666 = cm 8,666.
Avendo anche la misura dell'apotema possiamo applicare il teorema di Pitagora e trovare la misura del raggio della circonferenza circoscritta:
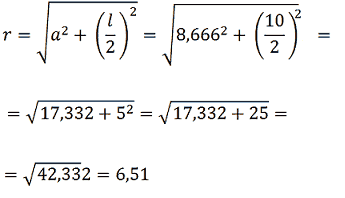
Abbiamo così trovato il raggio della circonferenza che misura cm 6,51.






