TEOREMA DI PITAGORA: DIMOSTRAZIONE

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Teorema di Pitagora: dimostrazione
• Triangolo rettangolo
• Quadrato
• Figure geometriche isoperimetriche ed equivalenti
• Criteri di congruenza dei triangoli rettangoli
• Figure equicomposte ed equiscomponibili
• Figure geometriche equivalenti e figure geometriche congruenti

Nella lezione precedente abbiamo visto un metodo per dimostrare il TEOREMA DI PITAGORA.

In questa lezione ne vedremo un altro.

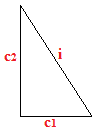
Disegniamo un qualsiasi TRIANGOLO RETTANGOLO. Indicheremo i suoi lati con le lettere:

• i = ipotenusa;
• c₁ = un cateto;
• c₂ = l'altro cateto.

Ora costruiamo DUE QUADRATI che abbiano come LATI le SOMME DEI DUE CATETI c₁ e c₂. Li chiamiamo rispettivamente Q_A e Q_B:

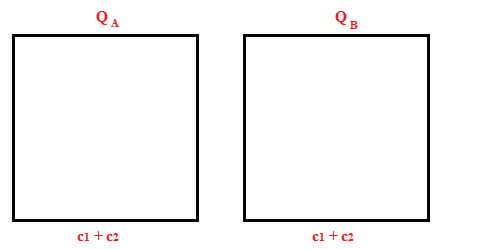
Q_Ae Q_B sono ISOPERIMETRICHE e CONGRUENTI.

Ora riportiamo sui lati dei due quadrati le misure dei cateti nel modo seguente (abbiamo indicato in viola c₁ e in verde c₂):

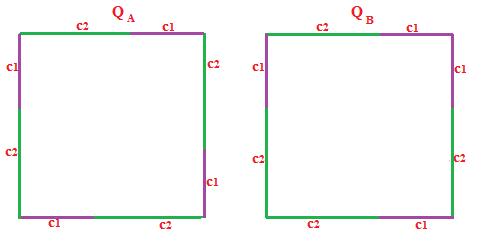
Nel primo quadrato Q_A uniamo i punti che separano i segmenti c₁ e c₂ nel modo che segue:

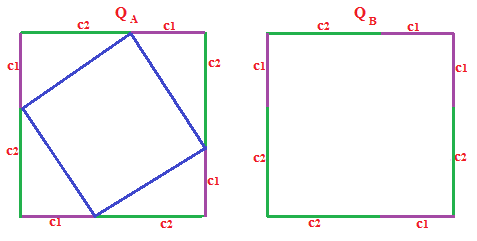
E ritagliamo il quadrato ottenuto che chiamiamo Q₁:

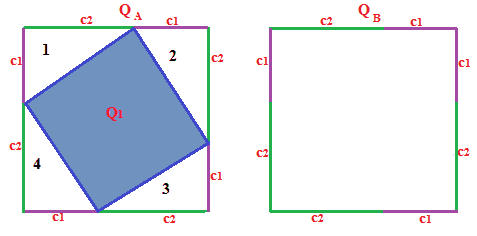
Ora esaminiamo i quattro triangoli che abbiamo ritagliato e che nella figura sopra abbiamo indicato con i numeri 1, 2, 3 e 4. Ognuno di essi ha come lati c₁ e c₂, cioè i cateti del triangolo di partenza. Dallo studio dei triangoli, sappiamo che se DUE TRIANGOLI RETTANGOLI hanno i DUE CATETI CONGRUENTI, allora sono CONGRUENTI. Quindi i quattro triangoli disegnati sono congruenti tra loro e congruenti con il triangolo di partenza.

Di conseguenza, il LATO del quadrato Q₁ non è altro che l'IPOTENUSA del triangolo dato.

Ora passiamo al secondo quadrato Q_B e uniamo i punti che separano i segmenti c₁ e c₂ nel modo seguente:

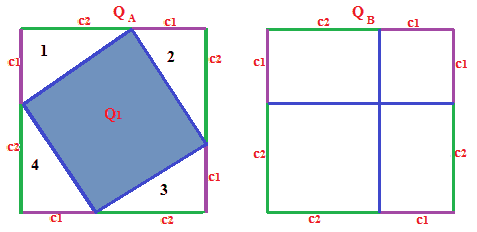
e ancora:

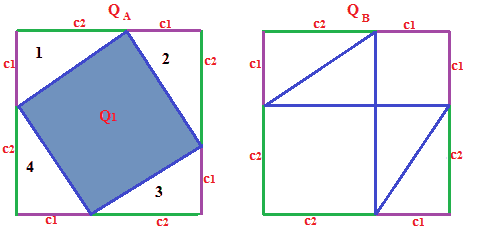
Ora ritagliamo i due quadrati ottenuti che indichiamo con Q₂ e Q₃:

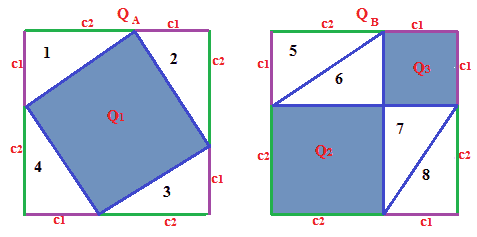
Ora esaminiamo i quattro triangoli che abbiamo ritagliato e che nella figura sopra abbiamo indicato con i numeri 5, 6, 7 e 8. Ognuno di essi ha come lati c₁ e c₂, cioè i cateti del triangolo di partenza. Come abbiamo già detto, se DUE TRIANGOLI RETTANGOLI hanno i DUE CATETI CONGRUENTI allora sono CONGRUENTI. Quindi i quattro triangoli disegnati sono congruenti tra loro e congruenti con il triangolo di partenza.

I due quadrati ottenuti Q₂ e Q₃, come è evidente dalla figura sopra, hanno come lati rispettivamente il cateto c₁ e c₂, cioè i cateti del triangolo di partenza.

Quindi, se al quadrato Q_A togliamo i triangoli 1, 2,3 e 4 otteniamo Q₁. Cioè:

Q₁ = Q_A - (1 + 2 + 3 + 4).

Se al quadrato Q_B togliamo i triangoli 5, 6, 7 e 8 otteniamo la somma di Q₂ + Q₃. Cioè:

Q₂ + Q₃ = Q_B - (5 + 6 + 7 + 8).

Abbiamo detto che:

• i due quadrati Q_A e Q_B sono EQUIVALENTI;
• i triangoli 1, 2, 3, 4 sono tutti CONGRUENTI tra loro e con il triangolo di partenza;
• i triangoli 5, 6, 7 e 8 sono tutti CONGRUENTI tra loro e con il triangolo di partenza;
• di conseguenza i triangoli 1, 2, 3, 4, 5, 6, 7 e 8 sono tutti CONGRUENTI tra loro.

Dallo studio dell'area dei poligoni sappiamo che FIGURE che sono la SOMMA o la DIFFERENZA di PARTI RISPETTIVAMENTE CONGRUENTI sono EQUIVALENTI.

Quindi essendo

Q₁ = Q_A - (1 + 2 + 3 + 4).

Q₂ + Q₃ = Q_B - (5 + 6 + 7 + 8).

ed essendo:

• Q_A e Q_B EQUIVALENTI;
• i triangoli 1, 2,3,4 , 5, 6, 7 e 8 CONGRUENTI tra loro

anche

Q₁ è CONGRUENTE con Q₂+Q₃.

Quindi abbiamo dimostrato che in OGNI TRIANGOLO RETTANGOLO, il QUADRATO costruito sull'IPOTENUSA è EQUIVALENTE alla SOMMA dei QUADRATI costruiti sui DUE CATETI.

Lezione precedente - Lezione successiva

Indice degli argomenti sul teorema di Pitagora

Pubblicità/Advertising