TEOREMA DI PITAGORA E ROMBO
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Le formule inverse del teorema di Pitagora
- Rombo
- Figure geometriche equivalenti e figure geometriche congruenti
- Diagonale di un poligono
- Triangolo rettangolo
- Area del rombo
Disegniamo un ROMBO ABCD:
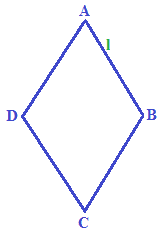
Ricordiamo che i lati l del rombo sono tutti congruenti tra loro.
Ora disegniamo le DIAGONALI del rombo che chiameremo d1 e d2:
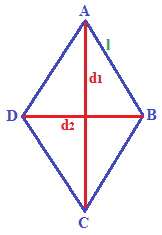
Le due DIAGONALI DIVIDONO il rombo in quattro TRIANGOLI RETTANGOLI congruenti.
I quattro triangoli rettangoli hanno:
- come CATETI, rispettivamente, metà della diagonale maggiore e metà della diagonale minore, cioè d1/2 e d2/2;
- come IPOTENUSA il lato l.
Di conseguenza, applicando il teorema di Pitagora possiamo scrivere:
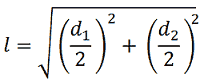
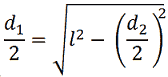
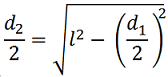
Esempio:
un rombo ha una delle diagonali e il lato lunghi rispettivamente cm 20 e cm 18. Calcolare l'are del rombo.
L'area del rombo la si ottiene moltiplicando la diagonale maggiore per la diagonale minore e dividendo il prodotto per 2, ovvero:
A = (d1 x d2)/ 2.
Ora noi conosciamo la misura di una delle diagonali, ma non dell'altra. Sappiamo, però, la misura del lato, quindi, applicando il teorema di Pitagora possiamo trovare la diagonale mancante.
Avremo:
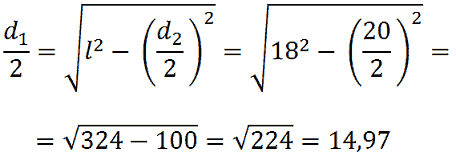
Se d1/2 misura cm 14,97 significa che d1 misura:
d1 = cm 14,97 x 2 = 29,94 cm.
Ora, conoscendo la misura di entrambe le diagonali, possiamo calcolare l'area. Ovvero:
A = (d1 x d2)/ 2 = (29,94 x 20)/ 2 = 299,40 cm2 .






