POTENZE AD ESPONENTE REALE

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Elevamento a potenza
• Casi particolari dell'elevazione a potenza
• Potenze di numeri relativi con esponente negativo
• Potenze con esponente frazionario
• L'insieme dei numeri reali
• Definizione di numeri reali
• L'insieme dei numeri interi relativi
• L'insieme dei numeri razionali relativi
• L'insieme dei numeri razionali relativi

Nelle nostre lezioni abbiamo imparato a conoscere vari tipi di potenze e più precisamente:

• le POTENZE di un NUMERO REALE, diverso da zero, con ESPONENTE INTERO POSITIVO.

  Esempio:

  
  
  

  
  
  

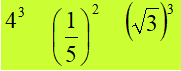
  Si tratta di potenze del tipo

  aⁿ

  che si risolvono moltiplicandoa per se stesso per n volte

  a = a x a x a.....x a (n volte)

  
  
  
• le POTENZE di un NUMERO REALE, diverso da zero, con ESPONENTE INTERO NEGATIVO.

  Esempio:

  
  
  

  
  
  

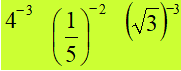
  Si tratta di potenze del tipo

  a^-n

  che si risolvono ponendo

  a^-n = 1/ (aⁿ)

  
  
  
• le POTENZA di un NUMERO REALE POSITIVO con ESPONENTE RAZIONALE POSITIVO.

  Esempio:

  
  
  

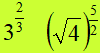
  Si tratta di potenze del tipo

  a^m/n

  che si risolvono ponendo

  
  
  

  
  
  
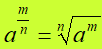
• le POTENZA di un NUMERO REALE POSITIVO con ESPONENTE RAZIONALE NEGATIVO.

  Esempio:

  
  
  

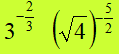
  Si tratta di potenze del tipo

  a^-m/n

  che si risolvono ponendo

  
  
  

  
  
  

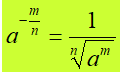
In questa lezione vogliamo parlare di POTENZE di un NUMERO REALE POSITIVO ad ESPONENTE IRRAZIONALE.

In altre parole ci troveremo di fronte a potenze del tipo:

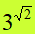
Cerchiamo di capirne il significato.

Iniziamo col dire che

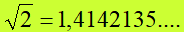
La radice di due è, quindi, un numero COMPRESO tra 1 e 2. Quindi possiamo dire che

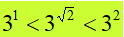
ovvero

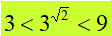
Ora, proseguendo su questo ragionamento, consideriamo anche il primo decimale (radice di 2 uguale 1,4). Possiamo dire, allora, che la radice di due è un numero COMPRESO tra 1,4 e 1,5. Quindi possiamo dire che

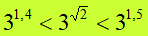
Ora esprimiamo 1,4 e 1,5 sotto forma di decimali, ovvero:

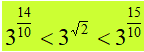
e semplificando gli esponenti possiamo scrivere

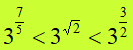
Ricordando che

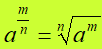
possiamo scrivere

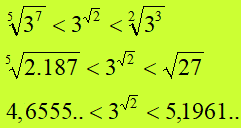
Andiamo avanti nel nostro ragionamento, consideriamo anche il secondo decimale (radice di 2 uguale 1,41). Possiamo dire, allora, che la radice di due è un numero COMPRESO tra 1,41 e 1,42. Quindi possiamo dire che

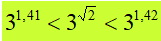
Procedendo come fatto in precedenza possiamo scrivere:

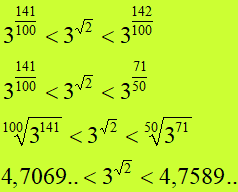
Andiamo ancora avanti e consideriamo anche il terzo decimale (radice di 2 uguale 1,414). Possiamo dire che la radice di due è un numero COMPRESO tra 1,414 e 1,415. Quindi possiamo dire che

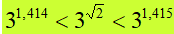
Procediamo così come abbiamo fatto prima:

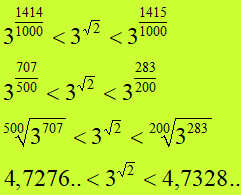
Andiamo ancora avanti e consideriamo anche il quarto decimale (radice di 2 uguale 1,4142). Possiamo dire che la radice di due è un numero COMPRESO tra 1,4142 e 1,4143. Quindi possiamo dire che

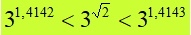
Ovvero:

Come possiamo notare l'intervallo di valori, nei quali è compreso tre elevato alla radice quadrata di due, si restringe sempre più. Se andiamo avanti con i nostri conteggi vedremo che gli intervalli successivi saranno

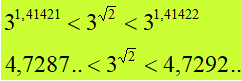
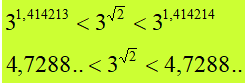
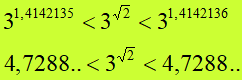
Abbiamo visto che il nostro intervallo si è ulteriormente ristretto. Da un certo punto in poi, le cifre decimali in comune sono sempre di più.

Possiamo, quindi, dire che le seguenti classi

definiscono la potenza

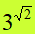
il cui valore approssimato ai centesimi è

4,72.

Quindi

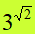
è un numero irrazionale poiché può essere immaginato come ELEMENTO SEPARATORE tra tutti i razionali che vengono prima e tutti i razionali che lo seguono. Perciò, questo numero, è un NUMERO REALE.

Chiaramente, quanto abbiamo detto può essere generalizzato a qualsiasi potenza di un numero reale positivo ad esponente irrazionale.

Ora facciamo alcune precisazioni.

La prima precisazione è che valgono, anche per le potenze di un numero reale positivo ad esponente irrazionale, le PROPRIETA' delle POTENZE studiate nell'ambito dei numeri naturali.

La seconda precisazione è che sono ESCLUSE le potenze con BASE NEGATIVA. Infatti abbiamo sempre parlato di potenze di un numero reale positivo ad esponente irrazionale. Vediamone il perché.

Supponiamo di voler calcolare

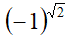
Ora sappiamo che

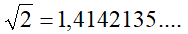
Quindi si tratta di fare:

(-1)^{1,4142135.....}

Possiamo anche scrivere

1,4142135... = 1 + 0,4 + 0,01 + 0,004 + 0,0002 + 0,00001 + 0,000003 +

0,0000005 + ......

Pertanto si può scrivere

(-1)^{1,4142135.....} = (-1)¹ · (-1)^0,4 · (-1)^0,01 · (-1)^0,004 · (-1)^0,0002 · (-1)^0,00001

· (-1)^0,000003 · (-1)^0,0000005 · .......

Ora, dovendo moltiplicare un numero infinito di fattori tutti negativi, come facciamo a sapere se il risultato sarà positivo o negativo? Per questa ragione si escludono le potenze con base negativa.

Si ricorda infine che, per

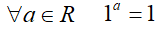
che si legge

per qualunque a appartenente ai reali, 1 elevato ad a è uguale ad 1.

Lezione successiva

Indice degli argomenti su esponenziali e logaritmi

Pubblicità/Advertising