I LOGARITMI: DEFINIZIONE
Immaginiamo di avere
52 = 25.
Ci troviamo di fronte a 3 numeri: 5, 2, 25. Vediamo in che modo possiamo calcolarne uno conoscendo il valore degli altri due.
Supponiamo di avere
52 = x
in altre parole non conosciamo quanto vale 5 alla seconda. Per trovare il valore della nostra x sarà sufficiente calcolare la POTENZA , cioè calcolare
5 · 5 = 25.
Adesso consideriamo, invece, il caso in cui sappiamo che un certo numero (la nostra x) elevato alla seconda, dà come risultato 25. In altre parole sappiamo che:
x2 = 25.
Per trovare il valore della nostra x, dobbiamo estrarre la RADICE quadrata di 25. Cioè:
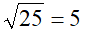
E se invece noi sappiamo che 5, elevato ad un certo numero x, dà come risultato 25, come facciamo a trovare il valore di x? Cioè:
5x = 25.
Per trovare il valore al quale dobbiamo elevare 5 per ottenere 25 dobbiamo usare i LOGARITMI. E dobbiamo scrivere:
x = log5 25
che si legge
x è uguale al logaritmo in base 5 di 25.
Generalizzando possiamo dire che, se
ax = b
allora avremo che
x = loga b
che si legge
x è uguale al logaritmo in base a di b.
Ora facciamo alcune precisazioni.
Come abbiamo visto parlando della funzione esponenziale, affinché ax abbia un significato reale è NECESSARIO che
a > 0
e
a ≠ 1.
Ora, se a è sempre positivo, elevando ad un qualsiasi numero reale x, otterremo un valore di b sempre positivo, cioè
b > 0.
Quindi, l'uguaglianza
ax = b
sussiste sempre a condizione che
a > 0
a ≠ 1
b > 0.
Quando sono verificate queste tre condizioni, l'equazione esponenziale ammette una ed una sola soluzione che potrà essere:
- reale razionale.
Esempio:
2x = 8
x = 3;
- reale irrazionale.
Esempio:
2x = 5
2 < x < 3
dato che
22 = 4
23 = 8.
La soluzione irrazionale dell'equazione
ax = b
si indica con
x = loga b
con
a > 0
a ≠ 1
b > 0.
Quindi possiamo dire che il LOGARITMO in base a (con a maggiore di zero e diverso da 1) di un numero b (anch'esso maggiore di zero) è l'ESPONENTE x da dare ad a per ottenere b.
Ora precisiamo che
- a si dice BASE del LOGARITMO;
- b si dice ARGOMENTO del LOGARITMO;
- c è il VALORE del LOGARITMO.







