POTENZE DI NUMERI RELATIVI CON ESPONENTE NEGATIVO
- I numeri relativi
- Rappresentazione grafica numeri relativi
- Operazioni con i numeri relativi
- Potenze di numeri relativi
- Proprietà delle potenze di numeri relativi
- Frazioni equivalenti
- Inverso di una frazione
Supponiamo di avere la seguente frazione:
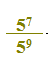
Come sappiamo una frazione può essere trasformata in un'altra equivalente, moltiplicando o dividendo sia il numeratore che il denominatore per uno stesso numero diverso da zero.
Vogliamo, allora, trasformare la nostra frazione in un'altra equivalente e per fare questo dividiamo numeratore e denominatore per 57, come segue:
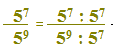
A questo punto eseguiamo la divisione posta a numeratore e quella posta a denominatore.
A numeratore dovremo eseguire 57 : 57. Ovviamente, poiché si tratta di dividere un numero per se stesso, il risultato sarà 1.
A denominatore dovremo eseguire 59 : 57. Per le proprietà delle potenze dobbiamo eseguire il quoziente di due potenze aventi la stessa base.
Esso è uguale ad una potenza che ha per base la stessa base, e per esponente la differenza degli esponenti. Quindi
59-7.
Per cui possiamo scrivere:
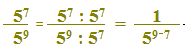
Eseguendo quando indicato a denominatore, abbiamo:
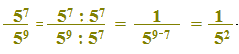
Quindi possiamo affermare che
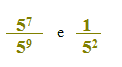
sono due frazioni equivalenti tra loro.
Ora proviamo a scrivere la prima frazione (57/59) in modo diverso.
Possiamo, cioè, scrivere:
57 : 59.
Anche in questo caso ci troviamo di fronte al quoziente di due potenze aventi la stessa base. Esso è uguale ad una potenza che ha per base la stessa base, e per esponente la differenza degli esponenti. Quindi:
57 : 59 = 57-9 = 5-2 .
Quindi possiamo dire che
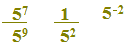
sono tre modi diversi di scrivere lo stesso valore.
Ora osserviamo meglio questi tre valori e in particolare gli ultimi due.
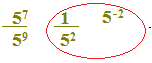
Possiamo quindi affermare che scrivere:
5-2
e scrivere
1/52
è
esattamente la STESSA COSA.
Quindi possiamo dire che la potenza ad esponente negativo è uguale ad una frazione che ha per numeratore l'unità e per denominatore la potenza della stessa base con esponente positivo.
Esempio:
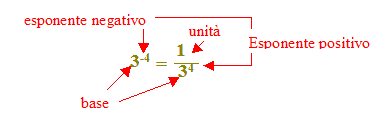
e ancora:
Più in generale, quindi, possiamo scrivere:
Le potenze con ESPONENTE INTERO NEGATIVO godono di tutte le proprietà delle POTENZE AD ESPONENTE INTERO POSITIVO.
Quindi valgono le seguenti proprietà:
- Il
prodotto di due o più potenze aventi la stessa base è
una potenza della stessa base con esponente uguale alla
somma degli esponenti.
Quindi:
a-m a-n = a (-m)+(-n) = a -m-n
Esempio:
- Il
quoziente di due o più potenze aventi la stessa base è
una potenza della stessa base con esponente uguale alla
differenza degli esponenti
Quindi:
a-m : a-n = a (-m)-(-n) = a-m+n
Esempio:
- La
potenza di una potenza è una potenza che ha per base la stessa
base e per esponente il prodotto degli esponenti.
Quindi:
(a-m)-n = a (-m)(-n)
Esempio:
(-3-2)-3 = (-3)(-2)(-3) = (-3)6 = +729.
- Il
prodotto tra due o più potenze aventi gli stessi
esponenti è uguale ad una potenza che ha per base il prodotto
delle basi e per esponente lo stesso esponente.
Quindi:
a-m b-m = (a b)-m
Esempio:
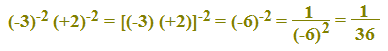
- Il
quoziente tra due potenze aventi gli stessi esponenti
è uguale ad una potenza che ha per base il quoziente delle
basi e per esponente lo stesso esponente.
Quindi:
a-m : b-m = (a : b)-m .
Esempio:
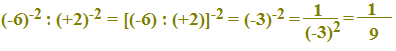
Le proprietà appena viste VALGONO ANCHE per le operazioni su potenze di numeri relativi che hanno ALCUNI ESPONENTI POSITIVI e ALTRI ESPONENTI NEGATIVI.
Esempio:
(-2)5 : (-2)-3 = (-2)5-(-3) = (-2)5+3 = (-2)8 = +256.
- Esercizio 47 - Potenze di numeri relativi
- Esercizio 48 - Potenze di numeri relativi
- Esercizio 49 - Potenze di numeri relativi






