EQUAZIONI OMOGENEE DI SECONDO GRADO IN SENO E COSENO
- Equazioni goniometriche
- Grado di un polinomio
- Equazioni goniometriche elementari del tipo sen x = a
- Equazioni goniometriche elementari del tipo cos x = b
- Equazioni goniometriche elementari del tipo tan x = c
- Equazioni lineare in seno e coseno
Proseguiamo l'esame delle EQUAZIONI GONIOMETRICHE e della loro risoluzione occupandoci, in questa lezione, delle EQUAZIONI OMOGENEE DI SECONDO GRADO IN SENO E COSENO.
Ricordiamo che un'equazione si dice OMOGENEA quando TUTTI i suoi TERMINI sono dello STESSO GRADO.
Queste equazioni si presentano nella forma:
a sen2 x + b sen x cos x + c cos2 x = 0.
Per risolvere questo tipo di equazioni dobbiamo distinguere tre casi:
- il primo caso si ha quando a = 0;
- il secondo caso si ha quando c = 0;
- il terzo ed ultimo caso si ha quando a ≠ 0 e c ≠ 0.
Partiamo dal primo caso:
a = 0.
L'equazione diventa:
b sen x cos x + c cos2 x = 0.
Per risolvere questa equazione METTIAMO IN EVIDENZA cos x ed otteniamo:
cos x (b sen x + c cos x) = 0
L'equazione così scritta può essere risolta grazie alla LEGGE DI ANNULLAMENTO DEL PRODOTTO. Pertanto, le soluzioni sono date da:
cos x = 0
oppure
b sen x + c cos x = 0
o entrambi nulli
La prima equazione
cos x = 0
è un'EQUAZIONE GONIOMETRICA ELEMENTARE NEL COSENO che si risolve nei modi visti in una precedente lezione.
La seconda equazione
b sen x + c cos x = 0
è un'EQUAZIONE LINEARE IN SENO E COSENO nella quale il termine noto è uguale a zero: anche la risoluzione di questo tipo di equazione è stata vista in una precedente lezione.
Secondo caso:
c = 0.
L'equazione diventa:
a sen x2 + b sen x cos x = 0.
Per risolvere questa equazione METTIAMO IN EVIDENZA sen x ed otteniamo:
sen x (a sen x + b cos x) = 0
Anche questa equazione può essere risolta grazie alla LEGGE DI ANNULLAMENTO DEL PRODOTTO. Quindi, le soluzioni sono date da:
sen x = 0
oppure
a sen x + b cos x = 0
o entrambi nulli
La prima equazione
sen x = 0
è un'EQUAZIONE GONIOMETRICA ELEMENTARE NEL SENO che si risolve nei modi visti in una precedente lezione.
La seconda equazione
a sen x + b cos x = 0
è sempre un'EQUAZIONE LINEARE IN SENO E COSENO nella quale il termine noto è uguale a zero. Come abbiamo detto prima, abbiamo già visto in una precedente lezione come si risolve.
Terzo caso: si ha quando sia a che c sono DIVERSI da ZERO. In altre parole
a ≠ 0 e c ≠ 0
In questo caso la soluzione dell'equazione la cerchiamo andando a DIVIDERE primo e secondo membro per cos2 x.
Possiamo farlo senza problemi poiché sicuramente il coseno di x è diverso da zero.
Infatti, quando
a ≠ 0
sicuramente
cos2 x ≠ 0.
Vediamo il perché.
Noi sappiamo che, quando il coseno di x è uguale a zero, sicuramente il seno di x è diverso da zero. Infatti:
- il coseno di x è uguale a zero, quando x è uguale a π/2, ma quando
l'angolo è pari a π/2 il seno è uguale ad 1. Quindi, se x = π/2,
fosse una soluzione della nostra equazione a primo membro avremmo:
a sen2 x + b sen x cos x + c cos2 x
a · (1)2 + b · 1 · 0 + 0
a · 1 + 0 + 0
che chiaramente è diverso da zero;
- il coseno di x è uguale a zero, anche quando x è uguale a 3π/2, ma quando
l'angolo è pari a 3π/2 il seno è uguale a -1. Quindi, se x = 3π/2,
fosse una soluzione della nostra equazione a primo membro avremmo:
a sen2 x + b sen x cos x + c cos2 x
a · (-1)2 + b · (-1) · 0 + 0
a · 1 + 0 + 0
che chiaramente è diverso da zero.
Quindi, possiamo dire che sicuramente cos x = 0 non è soluzione della nostra equazione e, pertanto, possiamo tranquillamente dividere l'equazione per cos2 x. E avremo:
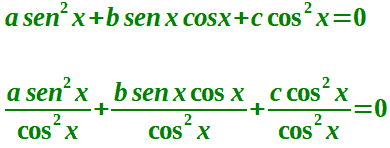
Semplificando possiamo scrivere:
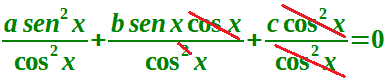
A questo punto andiamo a SOSTITUIRE, al posto del rapporto tra il seno e il coseno di x, la sua TANGENTE.
a tan2 x + b tan x + c = 0
Quella che abbiamo ottenuto è una EQUAZIONE DI SECONDO GRADO NELLA TANGENTE che si risolve ponendo:
y = tan x
in modo da avere:
a y2 + b y + c = 0
Questa equazione la risolviamo con la nota formula:
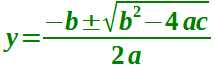
Una volta trovato il valore di y andremo a sostituirlo nella equazione:
y = tan x
andando a risolvere quella che è una EQUAZIONE GONIOMETRICA ELEMENTARE NELLA TANGENTE.
Nella prossima lezione andremo a vedere alcuni esempi di risoluzione delle equazioni omogenee di secondo grado in seno e coseno.






