ESEMPI DI RISOLUZIONE DI EQUAZIONI LINEARI IN SENO E COSENO CON IL METODO DELL'ANGOLO AGGIUNTO
- Equazioni goniometriche elementari del tipo sen x = a
- Equazioni lineari in seno e coseno
- Equazioni lineari in seno e coseno: metodo dell'angolo aggiunto
Nella lezione precedente abbiamo visto in cosa consiste il METODO DELL'ANGOLO AGGIUNTO nella soluzione delle EQUAZIONI LINEARI IN SENO E COSENO.
In questa lezione vedremo degli esempi di applicazione di tale metodo.
Esempio 1:
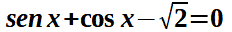
Per prima cosa calcoliamo r:
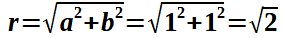
Quindi determiniamo il valore della tangente di α:
tan α = b/a = 1/1 = 1
Ora osserviamo che sia a che b sono POSITIVI quindi il lato termine di α si trova nel I QUADRANTE.
La tangente assume il valore 1 quando l'angolo è pari a π/4 e 5π/4, ma noi dobbiamo andare a prendere l'angolo α nel primo quadrante: quindi il valore che ci interessa è π/4.
A questo punto, ricordando che:
r sen (x + α) = - c
e sostituendo i valori trovati di r, α e c, possiamo scrivere:

Dividiamo entrambi i membri per la radice di due:
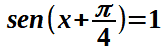
Il seno di un angolo è uguale ad 1 quando l'angolo è uguale a π/2 + 2kπ-
Quindi possiamo scrivere:
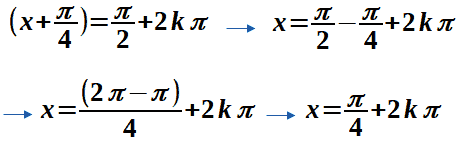
Abbiamo risolto la nostra equazione e trovato il valore di x.
Esempio 2:
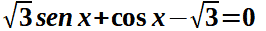
Iniziamo col calcolare r:
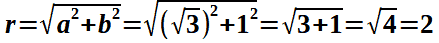
Quindi determiniamo il valore della tangente di α:
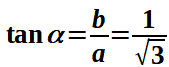
Razionalizziamo il denominatore della frazione ed otteniamo:
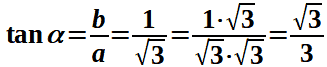
Anche in questo caso, sia a che b sono POSITIVI quindi il lato termine di α si trova nel I QUADRANTE.
Quindi andiamo a cercare nel primo quadante, l'angolo la cui tangente è pari alla radice di tre fratto tre: tale angolo è π/6.
Dato
r sen (x + α) = - c
sostituiamo i valori trovati di r, α e c, otteniamo:
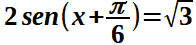
Dividiamo entrambi i membri per due:
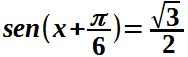
Il seno di un angolo è uguale alla radice di tre diviso 2 quando l'angolo è uguale a π/3 + 2kπ oppure (π - π/3) +2kπ ovvero 2/3 π.
Quindi possiamo scrivere: