DISEQUAZIONI DI SECONDO GRADO PARAMETRICHE
- Disequazioni di secondo grado
- Disequazioni razionali intere di secondo grado
- Come si risolvono le disequazioni intere di secondo grado
- Risoluzione di disequazioni intere di secondo grado
- Disequazioni intere letterali
- Disequazioni di secondo grado parametriche
- Disequazioni di secondo grado parametriche
- Esercizi con disequazioni parametriche di secondo grado
Dopo aver introdotto, nella lezione precedente, le DISEQUAZIONI DI SECONDO GRADO PARAMETRICHE, in questa lezione cercheremo di capire come si risolvono partendo da quelle nelle quali il PARAMETRO NON e' presente nel PRIMO COEFFICIENTE, ma è presente solamente nel secondo coefficiente o nel termine noto o in entrambi.
Cerchiamo di capire come procedere ricorrendo ad un esempio:
2x2 + x - a ≥ 0
In questo caso il parametro a è presente solamente come termine noto.
Partiamo applicando la formula risolutiva:
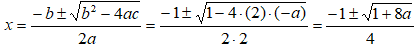
Il segno assunto dal determinante dipende dal valore assunto dal paramento a.
Andiamo a cercare gli zeri del determinante.
1+8a = 0
da cui otteniamo
8a = -1
a = -1/8.
Possiamo allora dire che
Δ > 0.
quando
a > -1/8.
In questo caso, la disequazione di partenza ammette due soluzioni distinte. Poiché il segno del primo coefficiente (+2) e il segno della disequazione (>) sono concordi, i valori da prendere sono quelli esterni alle soluzioni trovare, ovvero:
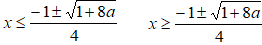
Avremo, invece, che
Δ = 0
quando
a = -1/8.
In questo caso, dato che il trinomio avrà lo stesso segno del primo coefficiente, esso sarà positivo. Poiché il segno della disequazione è maggiore, essa sarà sempre verificata per qualunque valore di x.
Infine
Δ < 0
quando
a < -1/8.
Anche in questo caso, dato che il trinomio avrà lo stesso segno del primo coefficiente, esso sarà positivo. Poiché il segno della disequazione è maggiore, la disequazione sarà sempre verificata per qualunque valore di x.
Passiamo ad un altro esempio:
3x2 - 2kx + 3 < 0.
In questo caso il parametro k è presente solamente nel secondo coefficiente.
Iniziamo applicando la formula risolutiva:
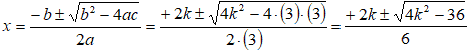
Il segno assunto dal determinante dipende dal valore assunto dal paramento k.
Andiamo a cercare gli zeri del determinante.
4k2 - 36 = 0
da cui otteniamo
4k2 = 36
k2 = 36/4
k2 = 9
k = ± 3.
Quindi il nostro determinante può essere scritto come prodotto dei due monomi (k + 3) e (k - 3), cioè:
Δ = (k + 3) (k - 3).
A questo punto vediamo come varia il valore del Δ al variare del valore di k.
Iniziamo a vedere quando
Δ > 0.
Questa situazione si verifica quando
(k + 3) (k - 3) > 0.
Studiamo il segno del nostro prodotto:
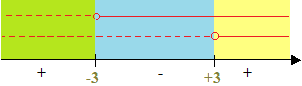
Il Δ è positivo quando
k < 3 k > 3.
Ora, quando il Δ è positivo, la nostra disequazione ammette due radici distinte. Esse sono
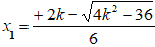
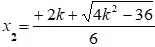
Poiché il segno del primo coefficiente della disequazione (+3) e il verso della disequazione (<), sono discordi, la disequazione è verificata per valori interni alle due radici trovate, cioè per
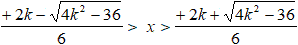
Ora vediamo quando
Δ = 0.
Questa situazione si verifica quando
(k + 3) (k - 3) = 0
cioè quando
k = ± 3.
Quando
k = -3
Poiché, in questo caso, il trinomio ha lo stesso segno del primo coefficiente, esso è positivo, mentre il segno della disequazione è minore. Quindi, quando
k = ± 3
la disequazione non è mai verificata.
Passiamo all'ultimo caso da esaminare, cioè al caso in cui
Δ < 0.
Questa situazione si verifica quando
(k + 3) (k - 3) < 0.
Riprendendo il grafico precedente

possiamo dire che ciò si verifica quando
-3 < k < +3.
In questi casi, il trinomio ha lo stesso segno del primo coefficiente. Quindi, dato che il primo coefficiente è positivo, il trinomio è positivo, mentre il segno della disequazione è minore. Quindi, la disequazione non è mai verificata.
Quindi possiamo dire che la nostra disequazione ammette soluzioni solamente se
k < 3 oppure k > 3
in questo caso le soluzioni sono
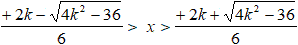
Per tutti gli altri valori di k la disequazione non ammette soluzioni.
Nella prossima lezione vedremo, invece, come si procede a risolvere delle disequazioni di secondo grado parametriche, quando il parametro compare come coefficiente del primo termine.






