DISEQUAZIONI DI SECONDO GRADO SPURIE
- Disequazioni di secondo grado
- Disequazioni razionali intere di secondo grado
- Come si risolvono le disequazioni intere di secondo grado
- Risoluzione di disequazioni intere di secondo grado
- Disequazioni di secondo grado incomplete
- Disequazioni di secondo grado pure
- Disequazioni di secondo grado monomie
- Raccoglimento a fattor comune
- Disequazioni fratte
Continuiamo il nostro esame delle disequazioni di secondo grado incomplete e vediamo come si risolvono le disequazione che si presentano nella forma
ax2 + bx > 0
oppure nella forma
ax2 + bx < 0.
Queste disequazioni sono dette DISEQUAZIONI di SECONDO GRADO SPURIE e sono caratterizzate dalla assenza del termine noto c.
Vediamo come vanno risolte, prendendo in considerazione la disequazione
ax2 + bx > 0.
Ovviamente ciò che diremo varrà, con le opportune modifiche, anche nel caso in cui il segno della disequazione sia minore (<) oppure maggiore uguale (≥) o minore uguale (≤).
Per risolvere la nostra disequazione dobbiamo:
- METTERE
in EVIDENZA la x
x (ax + b) > 0
- RISOLVERE
separatamente le DUE DISEQUAZIONI
x > 0
e
ax + b > 0
- STUDIARE il SEGNO del PRODOTTO e cercare i valori della x che lo rendono positivo.
Vediamo un esempio.
4x2 + 2x > 0.
Ci troviamo di fronte ad una disequazione di secondo grado spuria perché manca il termine noto.
Effettuiamo il raccoglimento a fattore comune. In questo caso non mettiamo in evidenza solo la x, ma mettiamo in evidenza 2x dato che i coefficiente 4 e 2 sono entrambi divisibili per 2:
2x (2x + 1) > 0.
Ora andiamo a risolvere separatamente:
2x > 0
2x + 1 > 0.
Avremo:
2x > 0 --> x > 0
2x + 1 > 0 --> 2x > - 1 --> x > -1/2.
Riportiamo i due risultati su un grafico e procediamo con lo studio dei segni:
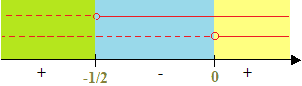
La nostra disequazione è positiva quando:
x < -1/2
x > 0.
Passiamo ad un altro esempio:
x2 - 3x < 0.
Mettiamo in evidenza la x:
x (x - 3) < 0.
Ora andiamo a risolvere separatamente:
x > 0
x - 3 > 0.
Avremo:
x > 0
x - 3 > 0 --> x > 3.
Riportiamo i due risultati su un grafico e procediamo con lo studio dei segni:
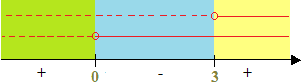
La nostra disequazione è negativa quando:
0 < x < 3.
Vediamo un ultimo esempio:
-5x2 + 10x≥ 0.
Mettiamo in evidenza 5x:
5x (-x + 2) ≥ 0.
Ora andiamo a risolvere separatamente:
5x ≥ 0
-x + 2 ≥ 0.
Avremo:
5x ≥ 0 --> x ≥ 0
-x +2 ≥ 0 --> x -2 ≤ 0 ---> x ≤ 2.
Riportiamo i due risultati su un grafico e procediamo con lo studio dei segni:
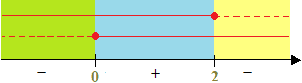
La nostra disequazione è positiva quando:
0 ≤ x ≤ 2.
Gli estremi vanno compresi nella soluzione dato che, quando x = 0, uno dei due fattori si annulla e, per la legge di annullamento del prodotto, tutto il prodotto sarà uguale a zero, e siccome noi cerchiamo i valori di x per i quali la disequazione è positiva o uguale a zero, tale valore va compreso nelle soluzioni ammissibili. La stessa cosa accade quando x = 2.






