IPERBOLE OMOGRAFICA: COME APPLICARE LE FORMULE
- L'iperbole
- Equazione dell'iperbole
- Asintoti dell'iperbole
- Iperbole traslata
- Iperbole equilatera riferita agli assi
- Iperbole equilatera riferita ai suoi asintoti
- Funzione omografica
- Elementi dell'iperbole omografica
Nella lezione precedente ci siamo occupati dell'iperbole omografica e delle sue formule. Vediamo ora un esempio di applicazione di tali formule.
Esempio:
sia
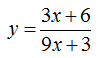
una iperbole omografica di cui vogliamo sapere gli asintoti, i fuochi e i vertici.
Ricordando che l'equazione dell'iperbole omografica è del tipo:
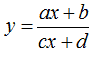
nel nostro caso avremo:
a = 3
b = 6
c = 9
d = 3.
Ora sappiamo che gli asintoti sono
x = -d/c
e
y = a/c.
Quindi, nel nostro caso, avremo:
x = -d/c = -3/9 = -1/3
e
y = a/c = 3/9 = 1/3.
Passiamo a determinare il valore di k ricordando che
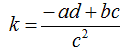
avremo
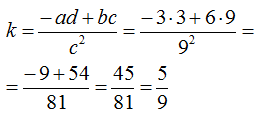
Poiché
k > 0
i vertici saranno
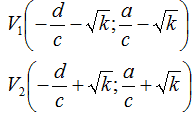
da cui
-d/c = -3/9 = -1/3
a/c = 3/9 = 1/3
quindi
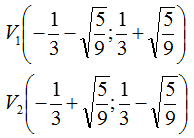
I fuochi sono
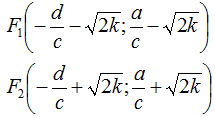
quindi
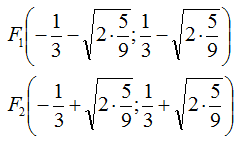
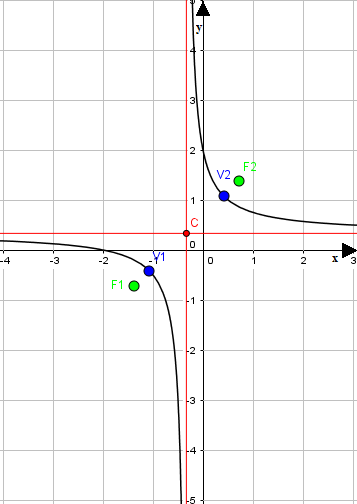
Ecco, graficamente, come si presenta la nostra iperbole: