IPERBOLE TRASLATA
- L'iperbole
- Equazione dell'iperbole
- Elementi dell'iperbole
- Assi cartesiani ortogonali
- Rette parallele
- Traslazione degli assi cartesiani
Nelle lezioni precedenti abbiamo sempre preso in esame l'iperbole canonica, ovvero l'iperbole che ha i fuochi su uno dei due assi cartesiani e il centro di simmetria nell'origine degli assi:
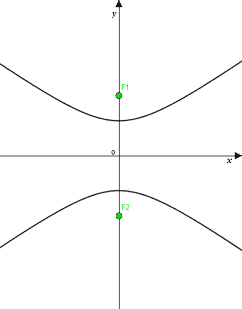
oppure
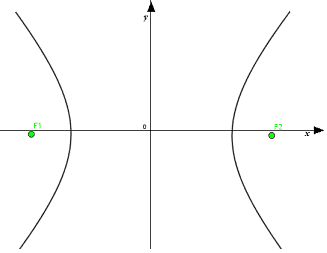
Può capitare, però, di trovarsi di fronte ad un'iperbole con CENTRO DI SIMMETRIA DIVERSO rispetto all'ORIGINE DEGLI ASSI. Si parla, in questi casi, di IPERBOLE TRASLATA.
Più precisamente parliamo di IPERBOLE TRASLATA quando gli ASSI del suo sistema di riferimento sono PARALLELI rispetto agli ASSI CARTESIANI.
Andiamo a disegnare un'iperbole traslata.
Disegniamo, in arancio, gli assi dell'iperbole in modo tale che:
- essi siano paralleli rispetto agli assi cartesiani;
- il punto P0 sia il punto di intersezione degli assi disegnati;
- il punto P0 rappresenti il centro di simmetria dell'iperbole.
Supponiamo che le coordinate del punto P0 siano
P0 (x0 ; y0)
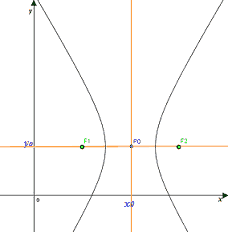
Ora vogliamo capire qual èl'EQUAZIONE dell'IPERBOLE TRASLATA.
Indichiamo con X e Y gli assi aventi per origine il punto P0 : tali assi sono gli assi di simmetria dell'iperbole:
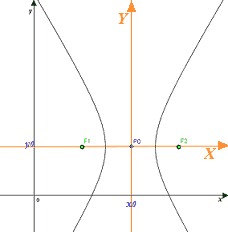
L'iperbole da noi disegnata non è altro che un'iperbole canonica rispetto al sistema di assi XP0 Y. Pertanto possiamo dire che la nostra iperbole ha, rispetto al sistema di assi XP0 Y,un'equazione della forma
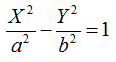
A noi, però, interessa sapere quale forma assume la nostra equazione sul sistema iniziale di assi xOy.
Possiamo facilmente risolvere il problema ricordando le equazioni che ci permettono di passare alle coordinate del sistema xOy. Queste equazioni sono:
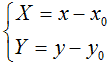
Effettuando le opportune sostituzioni avremo:
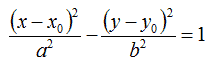
Quella che abbiamo appena scritto è l'EQUAZIONE dell'IPERBOLE TRASLATA,dove:
- x0 e y0 sono le coordinate del CENTRO dell'iperbole;
- a e b sono i due SEMIASSI dell'iperbole.
Ovviamente, nel caso in cui l'IPERBOLE ha i FUOCHI sull'ASSE parallelo all'asse delle ORDINATE, l'equazione dell'iperbole traslata sarà:
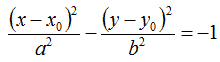
Nella prossima lezione vedremo come applicare le formule qui viste.






