ANGOLI NOTEVOLI: L'ANGOLO DI 60°
Continuiamo a vedere il valore che assumono le funzioni goniometriche nel caso degli ANGOLI NOTEVOLI andando ad occuparci dell'angolo di 60°, pari a π/3 RADIANTI.
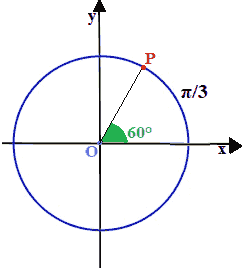
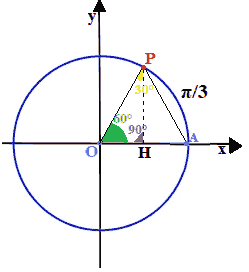
Costruiamo il triangolo PHO:
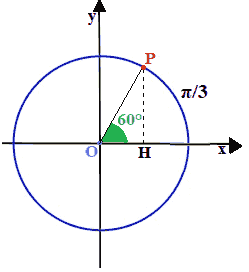
L'angolo con vertice in H è un angolo retto essondo il segmento PH perpendicolare all'asse delle ascisse.
Il triangolo è, quindi, un TRIANGOLO RETTANGOLO.
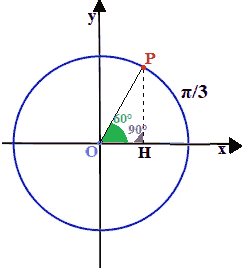
Noi sappiamo che l'angolo con vertice in O, ha um'ampiezza di 60° e che l'angolo con vertice in H, essendo retto, ha un'ampiezza di 90°. Sappiamo anche che la somma degli angoli interni di un triangolo è pari a 180°, quindi ne deduciamo che l'angolo con vertice in P ha un'ampiezza di 30° (infatti 180° - 60° - 90° = 30°).
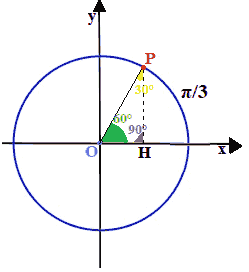
Ora ribaltiamo il triangolo PHO attorno al segmento PH. in modo da ottenere il triangolo PAO
Il triangolo PAO è un triangolo EQUILATERO dato che i suoi angoli misurano tutti e tre 60°.
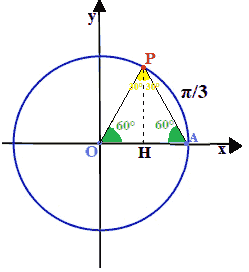
Noi sappiamo che il lato OP, essendo il raggio della circonferenza goniometrica, è uguale ad 1.
Poiché il triangolo è equilatero, tutti e tre i suoi lati, sono pari ad 1: quindi anche il segmento OA. Poiché il segmento OH è la metà di OA, esso è uguale a 1/2, che è anche il coseno dell'angolo di 60°.
Quindi:
cos 60° = 1/2
Passiamo al seno.
Il seno dell'angolo di 60° è dato dal segmento PH che non è altro che uno dei cateti del triangolo PHO. Quindi applichiamo il teorema di Pitagora e scriviamo:
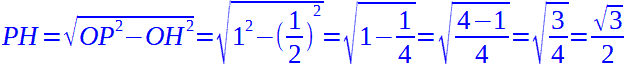
Pertanto:
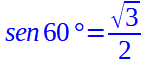
Ora che conosciamo seno e coseno, possiamo determinare la tangente che sarà pari a:
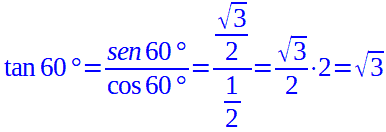
La cotangente dell'angolo di 60° è:
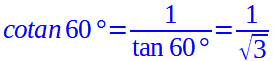
Eliminiamo la radice dal denominatore della frazione, moltiplicando numeratore e denominatore per la radice di tre, si ottiene:
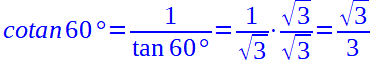
Andiamo a determinare la secante:
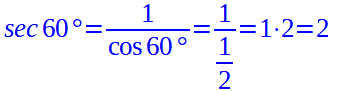
E finiamo calcolando la cosecante:
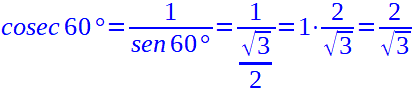
Moltiplichiamo numeratore e denominatore per la radice di tre ed abbiamo:
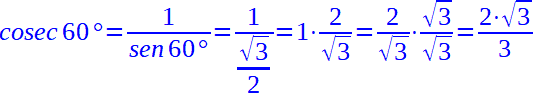
Nella prossima lezione vedremo i valori delle funzioni goniometriche relativi ad alcuni angoli del 2°, 3° e 4° quadrante.






